
【题目】已知三条直线l1:2x-y+a =" 0" (a>0),直线l2:-4x+2y+1 = 0和直线l3:x+y-1= 0,且l1与l2的距离是![]() .
.
(1)求a的值;
(2)能否找到一点P,使得P点同时满足下列三个条 件:
①P是第一象限的点;
②P 点到l1的距离是P点到l2的距离的![]() ;
;
③P点到l1的距离与P点到l3的距离之比是![]() ∶
∶![]() .若能,求P点坐标;若不能,说明理由.
.若能,求P点坐标;若不能,说明理由.
【答案】(1)a = 3;(2)P(![]() ,
,![]() )
)
【解析】试题分析:(1)由两平行直线之间距离公式列方程,解方程可得a的值(2)设P(x0,y0),由点到直线距离公式可得方程组,利用绝对值定义解方程组可得x0,y0
再根据点P在第一象限进行取舍
试题解析:解 (1)直线l2:2x-y-![]() =0,所以l1与l2间的距离为d=
=0,所以l1与l2间的距离为d=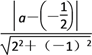 =
=![]() ,
,
即![]() =
=![]() ,又a>0,解得a=3.
,又a>0,解得a=3.
(2)假设存在P(x0,y0)满足条件②,则P在与l1,l2平行线l′:2x-y+c=0上, 且![]() =
=![]()
![]() ,即c=
,即c=![]() 或
或![]() ,
,
所以2x0-y0+![]() =0或2x0-y0+
=0或2x0-y0+![]() =0;
=0;
若P点满足条件③,由点到直线的距离公式,
有![]() =
=![]()
![]() ,|2x0-y0+3|=|x0+y0-1|,
,|2x0-y0+3|=|x0+y0-1|,
即x0-2y0+4=0或3x0+2=0;
由于点P在第一象限,所以3x0+2=0不可能.
联立方程2x0-y0+![]() =0和x0-2y0+4=0,解得
=0和x0-2y0+4=0,解得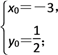 (舍去)
(舍去)
联立方程2x0-y0+![]() =0和x0-2y0+4=0,
=0和x0-2y0+4=0,
解得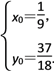 所以存在点P
所以存在点P![]() 同时满足三个条件.
同时满足三个条件.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知向量m=(cosx,-1),n=![]() ,函数f(x)=(m+n)·m.
,函数f(x)=(m+n)·m.
(1)求函数f(x)的最小正周期;
(2)已知a,b,c分别为△ABC内角A,B,C的对边,A为锐角,a=1,c=![]() ,且f(A)恰是函数f(x)在
,且f(A)恰是函数f(x)在![]() 上的最大值,求A,b和△ABC的面积.
上的最大值,求A,b和△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区以“绿色出行”为宗旨开展“共享单车”业务.该地区某高级中学一兴趣小组由9名高二级学生和6名高一级学生组成,现采用分层抽样的方法抽取5人,组成一个体验小组去市场体验“共享单车”的使用.问:
(Ⅰ)应从该兴趣小组中抽取高一级和高二级的学生各多少人;
(Ⅱ)已知该地区有![]() ,
, ![]() 两种型号的“共享单车”,在市场体验中,该体验小组的高二级学生都租
两种型号的“共享单车”,在市场体验中,该体验小组的高二级学生都租![]() 型车,高一级学生都租
型车,高一级学生都租![]() 型车.如果从组内随机抽取2人,求抽取的2人中至少有1人在市场体验过程中租
型车.如果从组内随机抽取2人,求抽取的2人中至少有1人在市场体验过程中租![]() 型车的概率.
型车的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知曲线
中,已知曲线![]() (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() ,曲线
,曲线![]() .
.
(1)求曲线![]() 与
与![]() 的交点
的交点![]() 的直角坐标;
的直角坐标;
(2)设点![]() ,
, ![]() 分别为曲线
分别为曲线![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市居民自来水收费标准如下:每户每月用水不超过4吨时,每吨为2.10元,当用水超过4吨时,超过部分每吨3.00元,某月甲、乙两户共交水费y元.已知甲、乙两用户该月用水量分别为5x,3x吨.
(1)求y关于x的函数;
(2)如甲、乙两户该月共交水费40.8元,分别求出甲、乙两户该月的用水量和水费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
某公司经销某产品,第![]() 天
天![]() 的销售价格为
的销售价格为![]() (
(![]() 为常数)(元∕件),第
为常数)(元∕件),第![]() 天的销售量为
天的销售量为![]() (件),且公司在第
(件),且公司在第![]() 天该产品的销售收入为
天该产品的销售收入为![]() 元.
元.
(1)求该公司在第![]() 天该产品的销售收入是多少?
天该产品的销售收入是多少?
(2)这![]() 天中该公司在哪一天该产品的销售收入最大?最大收入为多少?
天中该公司在哪一天该产品的销售收入最大?最大收入为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
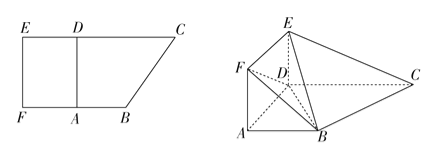
【题目】【2017银川一中模拟】如图,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=![]() CD=1.现以AD为一边向梯形外作矩形ADEF,然后沿边AD将矩形ADEF翻折,使平面ADEF与平面ABCD垂直.
CD=1.现以AD为一边向梯形外作矩形ADEF,然后沿边AD将矩形ADEF翻折,使平面ADEF与平面ABCD垂直.
(1)求证:BC⊥平面BDE;
(2)若点D到平面BEC的距离为![]() ,求三棱锥F-BDE的体积.
,求三棱锥F-BDE的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com