
分析 利用复数的几何意义,结合向量的性质进行判断即可.
解答 解:设复数z1、z2在复平面内对应的向量为$\overrightarrow{{Z}_{1}}$,$\overrightarrow{{Z}_{2}}$,
则由|z1+z2|=|z1-z2|,得|$\overrightarrow{{Z}_{1}}+\overrightarrow{{Z}_{2}}$|=|$\overrightarrow{{Z}_{1}}-\overrightarrow{{Z}_{2}}$|,
则以向量$\overrightarrow{{Z}_{1}}$,$\overrightarrow{{Z}_{2}}$为邻边的平行四边形为矩形,
则∠AOB的大小是90°,
故答案为:90°.
点评 本题主要考查复数几何意义的意义,根据条件转化为向量是解决本题的关键,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
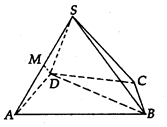 如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.
如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,-$\frac{9}{8}$) | B. | (3,-$\frac{7}{8}$) | C. | (5,-$\frac{9}{8}$) | D. | (4,-$\frac{5}{8}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${(-\frac{1}{2})^n}$ | B. | $-\frac{1}{2^n}$ | C. | $-{(-\frac{1}{2})^n}$ | D. | $-{(\frac{1}{2})^{n-1}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com