
【题目】已知椭圆![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,
, ![]() ,点
,点 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在斜率为2的直线![]() ,使得当直线
,使得当直线![]() 与椭圆
与椭圆![]() 有两个不同交点
有两个不同交点![]() 时,能在直线
时,能在直线![]() 上找到一点
上找到一点![]() ,在椭圆
,在椭圆![]() 上找到一点
上找到一点![]() ,满足
,满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
【答案】(1)![]() ;(2)不存在,理由见解析.
;(2)不存在,理由见解析.
【解析】试题分析:(1)由焦点坐标可得![]() ,再根据
,再根据![]() 及点
及点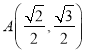 在椭圆
在椭圆![]() 上,可得
上,可得![]() ,进而可得椭圆的方程;(2)设直线
,进而可得椭圆的方程;(2)设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立可得
,与椭圆方程联立可得![]() ,与判别式为正可得
,与判别式为正可得![]() ,再根据平行四边形性质及韦达定理可得点
,再根据平行四边形性质及韦达定理可得点![]() 的纵坐标范围是
的纵坐标范围是![]() ,可判定点
,可判定点![]() 不在椭圆上,所以这样的直线
不在椭圆上,所以这样的直线![]() 不存在.
不存在.
试题解析:(1)设椭圆![]() 的焦距为
的焦距为![]() ,则
,则![]() ,
,
因此椭圆方程为![]()
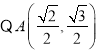 在椭圆上,
在椭圆上, 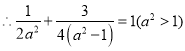 解得
解得![]()
故椭圆![]() 的方程为
的方程为![]() .
.
(2)假设存在这样的直线 设直线![]() 的方程为
的方程为![]() ,
,
设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 的中点为
的中点为![]() ,
,
由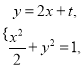 得
得![]() ,
,
所以![]() ,且
,且![]() ,则
,则![]() ,
,
![]()
![]()
由![]() 知四边形
知四边形![]() 为平行四边形,
为平行四边形,
而![]() 为线段
为线段![]() 的中点,因此,
的中点,因此, ![]() 也是线段
也是线段![]() 的中点,
的中点,
所以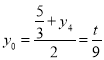 ,可得
,可得![]() ,
,
又![]() ,所以
,所以![]() ,
,
因此点![]() 不在椭圆上.
不在椭圆上.
所以这样的直线l不存在
【方法点晴】本题主要考查待定系数法求椭圆的标准方程、韦达定理以及解析几何中的存在性问题,属于难题.解决存在性问题,先假设存在,推证满足条件的结论,若结论正确则存在,若结论不正确则不存在,注意:①当条件和结论不唯一时要分类讨论;②当给出结论而要推导出存在的条件时,先假设成立,再推出条件;③当条件和结论都不知,按常规方法题很难时采取另外的途径.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】某校高一学生共有500人,为了了解学生的历史学习情况,随机抽取了50名学生,对他们一年来4次考试的历史平均成绩进行统计,得到频率分布直方图如图所示,后三组频数成等比数列.
(1)求第五、六组的频数,补全频率分布直方图;
(2)若每组数据用该组区间中点值(例如区间[70,80)的中点值是
75作为代表,试估计该校高一学生历史成绩的平均分;
(3)估计该校高一学生历史成绩在70~100分范围内的人数.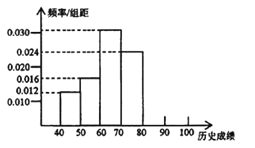
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 为参数
为参数![]() 和直线
和直线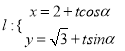
![]() 其中
其中![]() 为参数,
为参数, ![]() 为直线
为直线![]() 的倾斜角
的倾斜角![]() .
.
(1)当![]() 时,求圆上的点到直线
时,求圆上的点到直线![]() 的距离的最小值;
的距离的最小值;
(2)当直线![]() 与圆
与圆![]() 有公共点时,求
有公共点时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥V﹣ABCD中,底面ABCD是正方形,侧棱VA⊥底面ABCD,点E为VA的中点.
(Ⅰ)求证:VC∥平面BED;
(Ⅱ)求证:平面VAC⊥平面BED.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(0,2),斜率为k,圆Q:x2+y2﹣12x+32=0.
(1)若直线l和圆相切,求直线l的方程;
(2)若直线l和圆交于A、B两个不同的点,问是否存在常数k,使得![]() +
+![]() 与
与![]() 共线?若存在,求出k的值;若不存在,请说明理由.
共线?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率![]() ,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计
,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请200名同学,每人随机写下一个都小于1的正实数对(x,y);再统计两数能与1构成钝角三角形三边的数对(x,y)的个数m;最后再根据统计数m来估计
的值:先请200名同学,每人随机写下一个都小于1的正实数对(x,y);再统计两数能与1构成钝角三角形三边的数对(x,y)的个数m;最后再根据统计数m来估计![]() 的值.假如统计结果是m=56,那么可以估计
的值.假如统计结果是m=56,那么可以估计![]() __________.(用分数表示)
__________.(用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点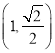 ,离心率为
,离心率为![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 的长轴的两个端点(
的长轴的两个端点(![]() 位于
位于![]() 右侧),
右侧),![]() 是椭圆在
是椭圆在![]() 轴正半轴上的顶点.
轴正半轴上的顶点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 和
和![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求出直线方程;如果不存在,请说明理由.
共线?如果存在,求出直线方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:函数y=log2(x2﹣2x)的单调增区间是[1,+∞),命题q:函数y=![]() 的值域为(0,1),下列命题是真命题的为( )
的值域为(0,1),下列命题是真命题的为( )
A.p∧q
B.p∨q
C.p∧(¬q)
D.¬q
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com