【题目】若数列
同时满足：①对于任意的正整数
， 
恒成立；②对于给定的正整数
， 
对于任意的正整数
恒成立，则称数列
是“
数列”.
（1）已知
判断数列
是否为“
数列”，并说明理由；
（2）已知数列
是“
数列”，且存在整数
，使得
， 
， 
， 
成等差数列，证明： 
是等差数列.
【答案】（1）是（2）见解析
【解析】试题分析：（1）根据定义验证两个条件是否成立，由于函数为分段函数，所以分奇偶分别验证（2）根据定义数列隔项成等差，再根据单调性确定公差相等，最后求各项通项，根据通项关系得数列
通项，根据等差数列证结论
试题解析：（1）当
为奇数时， 
，所以
.
.
当
为偶数时， 
，所以
.
.
所以，数列
是“
数列”.
（2）由题意可得： 
，
则数列
， 
， 
， 
是等差数列，设其公差为
，
数列
， 
， 
， 
是等差数列，设其公差为
，
数列
， 
， 
， 
是等差数列，设其公差为
.
因为
，所以
，
所以
，
所以
①，
②.
若
，则当
时，①不成立；
若
，则当
时，②不成立；
若
，则①和②都成立，所以
.
同理得： 
，所以
，记
.
设
，
则
.
同理可得： 
，所以
.
所以
是等差数列.
【另解】
，
，
，
以上三式相加可得： 
，所以
，
所以
，
，
，
所以
，所以
，
所以，数列
是等差数列.
长江作业本同步练习册系列答案科目：高中数学 来源： 题型：
【题目】已知圆
的标准方程为
，圆心为，直线
的方程为
，点
在直线上，过点作圆的切线
，
，切点分别为
，
．
（1）若
，试求点的坐标；
（2）若点的坐标为
，过作直线与圆交于
两点，当
时，求直线
的方程；
（3）求证：经过，，三点的圆必过定点，并求出所有定点的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
的前
项和为
，且满足
，
，设
，则以下四个命题：（1）
是等差数列；（2）
中最大项是
；（3）通项公式是
；（4）
.其中真命题的序号是______.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从数列
中取出部分项组成的数列称为数列的“子数列”.
（1）若等差数列的公差
，其子数列
恰为等比数列，其中
，
，
，求
；
（2）若
，
，判断数列
是否为的“子数列”，并证明你的结论.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】市政府招商引资，为吸引外商，决定第一个月产品免税，某外资厂该第一个月A型产品出厂价为每件10元，月销售量为6万件；第二个月，当地政府开始对该商品征收税率为
，即销售1元要征收
元）的税收，于是该产品的出厂价就上升到每件
元，预计月销售量将减少p万件.
（1）将第二个月政府对该商品征收的税收y（万元）表示成p的函数，并指出这个函数的定义域；
（2）要使第二个月该厂的税收不少于1万元，则p的范围是多少？
（3）在第（2）问的前提下，要让厂家本月获得最大销售金额，则p应为多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE，H是直角项点)来处理污水．管道越长，污水净化效果越好．设计要求管道的接口H是AB的中点，E，F分别落在线段BC，AD上．已知AB＝20米，AD＝
米，记∠BHE＝
．
（1）试将污水净化管道的长度L表示为的函数，并写出定义域；
（2）当取何值时，污水净化效果最好？并求出此时管道的长度L．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，椭圆
的左、右焦点分别为
，
，点
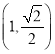在椭圆上．
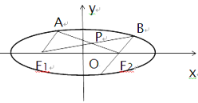
（1）求椭圆的方程；
（2）若A，B是椭圆上位于x轴上方的两点，直线
与直线
交于点P，
，求直线
的斜率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
