
【题目】 如图,在三棱锥
如图,在三棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求证![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(Ⅰ)略,(Ⅱ) ![]() ,(Ⅲ)
,(Ⅲ)![]()
【解析】 解法一
解法一
(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
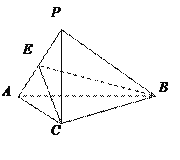
![]() ,
,
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
![]() .
.
(Ⅱ)![]() ,
, ![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
又![]() ,即
,即![]() ,且
,且![]() ,
,
![]() 平面
平面![]() .
.
取![]() 中点
中点![]() .连结
.连结![]() .
.
![]() ,
, ![]() .
.
![]() 是
是![]() 在平面
在平面![]() 内的射影,
内的射影,
![]() .
.
![]() 是二面角
是二面角![]() 的平面角.
的平面角.
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
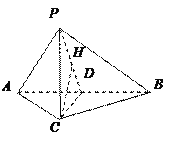
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
(Ⅲ)由(Ⅰ)知![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() .
.
过![]() 作
作![]() ,垂足为
,垂足为![]() .
.
![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
![]() 的长即为点
的长即为点![]() 到平面
到平面![]() 的距离.
的距离.
由(Ⅰ)知![]() ,又
,又![]() ,且
,且![]() ,
,
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
![]() .
.
在![]() 中,
中, ![]() ,
, ![]() ,
,
![]() .
.
![]() .
.
![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
解法二
(Ⅰ)![]() ,
, ![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
![]() ,
,
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
![]() .
.
(Ⅱ)如图,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() .
.
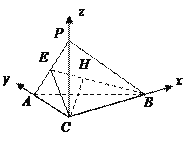 则
则![]() .
.
设![]() .
.
![]() ,
,
![]() ,
, ![]() .
.
取![]() 中点
中点![]() ,连结
,连结![]() .
.
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
![]() 是二面角
是二面角![]() 的平面角.
的平面角.
![]() ,
, ![]() ,
, ![]() ,
,
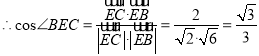 .
.
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
(Ⅲ)![]() ,
,
![]() 在平面
在平面![]() 内的射影为正
内的射影为正![]() 的中心
的中心![]() ,且
,且![]() 的长为点
的长为点![]() 到平面
到平面![]() 的距离.
的距离.
如(Ⅱ)建立空间直角坐标系![]() .
.
![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() .
.
![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】从甲、乙两种棉花中各抽测了25根棉花的纤维长度(单位: ![]() ) 组成一个样本,且将纤维长度超过315
) 组成一个样本,且将纤维长度超过315![]() 的棉花定为一级棉花.设计了如下茎叶图:
的棉花定为一级棉花.设计了如下茎叶图:

(1)根据以上茎叶图,对甲、乙两种棉花的纤维长度作比较,写出两个统计结论(不必计算);
(2)从样本中随机抽取甲、乙两种棉花各2根,求其中恰有3根一级棉花的概率;
(3)用样本估计总体,将样本频率视为概率,现从甲、乙两种棉花中各随机抽取1根,求其中一级棉花根数X的分布列及数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一辆汽车从![]() 市出发沿海岸一条笔直公路以每小时
市出发沿海岸一条笔直公路以每小时![]() 的速度向东均速行驶,汽车开动时,在
的速度向东均速行驶,汽车开动时,在![]() 市南偏东方向距
市南偏东方向距![]() 市
市![]() 且与海岸距离为
且与海岸距离为![]() 的海上
的海上![]() 处有一快艇与汽车同时出发,要把一份稿件交给这汽车的司机.
处有一快艇与汽车同时出发,要把一份稿件交给这汽车的司机.
(1)快艇至少以多大的速度行驶才能把稿件送到司机手中?
(2)在(1)的条件下,求快艇以最小速度行驶时的行驶方向与![]() 所成的角.
所成的角.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】扎花灯是中国一门传统手艺,逢年过节时常常在大街小巷看到各式各样的美丽花灯。现有一个花灯,它外围轮廓是由两个形状完全相同的抛物线绕着它们自身的对称轴旋转而来(如图),花灯的下顶点为![]() ,上顶点为
,上顶点为![]() ,
,![]() 米,在它的内部放有一个半径为
米,在它的内部放有一个半径为![]() 米的球形灯泡,球心
米的球形灯泡,球心![]() 在轴
在轴![]() 上,且
上,且![]() 米。若球形灯泡的球心
米。若球形灯泡的球心![]() 到四周轮廓上的点的最近距离是在下顶点
到四周轮廓上的点的最近距离是在下顶点![]() 处取到。建立适当的坐标系可得抛物线方程为
处取到。建立适当的坐标系可得抛物线方程为![]() ,则实数
,则实数![]() 的取值范围是_______
的取值范围是_______

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】江苏省淮阴中学科技兴趣小组在计算机上模拟航天器变轨返回试验.设计方案如图,航天器运行(按顺时针方向)的轨迹方程为![]() ,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以![]() 轴为对称轴、
轴为对称轴、![]() 为顶点的抛物线的实线部分,降落点为
为顶点的抛物线的实线部分,降落点为![]() .观测点
.观测点![]() 同时跟踪航天器,试问:当航天器在
同时跟踪航天器,试问:当航天器在![]() 轴上方时,观测点
轴上方时,观测点![]() ,
,![]() 测得离航天器的距离分别为多少时,应向航天器发出变轨指令?(变轨指令发出时航天器立即变轨)。
测得离航天器的距离分别为多少时,应向航天器发出变轨指令?(变轨指令发出时航天器立即变轨)。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以平面直角坐标系
为参数).以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,设直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,设直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 和直线
和直线![]() 的普通方程;
的普通方程;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求点
上任意一点,求点![]() 到直线
到直线![]() 的距离的最值.
的距离的最值.
【答案】(1)![]() ,
, ![]() ;(2)最大值为
;(2)最大值为![]() ,最小值为
,最小值为![]()
【解析】试题分析:(1)根据参数方程和极坐标化普通方程化法即易得结论![]() 的普通方程为
的普通方程为![]() ;直线
;直线![]() 的普通方程为
的普通方程为![]() .(2)求点到线距离问题可借助参数方程,利用三角函数最值法求解即可故设
.(2)求点到线距离问题可借助参数方程,利用三角函数最值法求解即可故设![]() ,
, ![]()
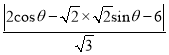
![]()
 .即可得出最值
.即可得出最值
解析:(1)根据题意,由 ,得
,得![]() ,
, ![]() ,
,
由![]() ,得
,得![]() ,
,
故![]() 的普通方程为
的普通方程为![]() ;
;
由![]() 及
及![]() ,
, ![]() 得
得![]() ,
,
故直线![]() 的普通方程为
的普通方程为![]() .
.
(2)由于![]() 为曲线
为曲线![]() 上任意一点,设
上任意一点,设![]() ,
,
由点到直线的距离公式得,点![]() 到直线
到直线![]() 的距离为
的距离为
![]()

![]()
 .
.
∵![]()
![]() ,
,
∴
 ,即
,即![]()
![]() ,
,
故点![]() 到直线
到直线![]() 的距离的最大值为
的距离的最大值为![]() ,最小值为
,最小值为![]() .
.
点睛:首先要熟悉参数方程和极坐标方程化普通方程的方法,第一问基本属于送分题所以务必抓住,对于第二问可以总结为一类题型,借助参数方程设点的方便转化为三角函数最值问题求解
【题型】解答题
【结束】
23
【题目】已知函数![]() ,
,![]() .
.
(1)解关于![]() 的不等式
的不等式![]() ;
;
(2)若函数![]() 的图象恒在函数
的图象恒在函数![]() 图象的上方,求
图象的上方,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,且相邻两对称轴间的距离为
为奇函数,且相邻两对称轴间的距离为![]()
(1)当![]() 时,求
时,求![]() 的单调递减区间;
的单调递减区间;
(2)将函数![]() 的图象沿
的图象沿![]() 轴正方向向右平移
轴正方向向右平移![]() 个单位长度,再把横坐标缩短为原来的
个单位长度,再把横坐标缩短为原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象,当
的图象,当![]() 时,求函数
时,求函数![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 也为抛物线
也为抛物线![]() 的焦点.(1)若
的焦点.(1)若![]() 为椭圆
为椭圆![]() 上两点,且线段
上两点,且线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2)若过椭圆![]() 的右焦点
的右焦点![]() 作两条互相垂直的直线分别交椭圆于
作两条互相垂直的直线分别交椭圆于![]() 和
和![]() ,设线段
,设线段![]() 的长分别为
的长分别为![]() ,证明
,证明![]() 是定值.
是定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com