Question

【题目】已知函数y=f（x）在定义域（﹣ ，3）内可导，其图像如图所示．记y=f（x）的导函数为y=f′（x），则不等式 ≤0的解集为 ．

Answer 1

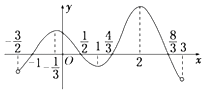
【答案】[2，3]∪[﹣ ，﹣ ]
【解析】解：不等式 ≤0，等价于 ①，或 ②．
由y=f（x）图像可知f（x）在[﹣ ，1]、[2，3]内递减，f′（x）≤0；
f（x）在[﹣ ，﹣ ]、[1，2]内递增，f′（x）≥0．
故由①可得x∈[2，3]，由②可得x∈[﹣ ，﹣ ]．
综上可得，不等式 ≤0的解集为[2，3]∪[﹣ ，﹣ ]，
所以答案是：[2，3]∪[﹣ ，﹣ ]．
【考点精析】认真审题，首先需要了解函数单调性的性质(函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集)，还要掌握导数的几何意义(通过图像,我们可以看出当点趋近于时，直线与曲线相切．容易知道，割线的斜率是，当点趋近于时，函数在处的导数就是切线PT的斜率k，即)的相关知识才是答题的关键．