练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】从中任取三个或三个以上的数，使其和为偶数的取法共有多少种？

    【答案】.

    【解析】

    由题意，取出的奇数必须是偶数个（包括不取奇数）,然后按照取出的数中奇数的个数分为9类分类计数，再相加即可得到答案.

    由题意，取出的奇数必须是偶数个（包括不取奇数）．

    （1）奇数一个都不取，则偶数可取个，共有种取法；

    （2）奇数取2个，则偶数可取个，共有种取法；

    （3）奇数取4个，则偶数可取个，共有种取法；

    （4）奇数取6个，则偶数可取个，共有种取法；

    （5）奇数取8个，则偶数可取个，共有种取法；

    （6）奇数取10个，则偶数可取个，共有种取法；

    （7）奇数取12个，则偶数可取个，共有种取法；

    （8）奇数取14个，则偶数可取个，共有种取法；

    （9）奇数取16个，则偶数可取个，共有种取法．

    所以所求取法共有.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知二次函数y=f1(x)的图象以原点为顶点且过点(1,1),反比例函数y=f2(x)的图象与直线y=x的两个交点间距离为8,f(x)= f1(x)+ f2(x).

    (Ⅰ) 求函数f(x)的表达式；

    (Ⅱ) 证明:当a>3时,关于x的方程f(x)= f(a)有三个实数解.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知

    （1）若a=1，且f(x)≥m在(0，+∞)恒成立，求实数m的取值范围；

    （2）当时，若x=0不是f(x)的极值点，求实数a的取值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一副扑克牌有52张（不包括大小王），求：

    （1）任取1张是红桃的概率；

    （2）任取2张是同花色的概率；

    （3）任取3张，至少有2张是同花色的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某厂能够生产甲、乙两种产品，已知生产这两种产品每吨所需的煤、电以及每吨的产值分别是：

    用煤（t）

    用电（kw）

    产值（千元）

    甲种产品

    70

    20

    80

    乙种产品

    30

    50

    110

    如果该厂每月至多供煤560t，供电450kw，问如何安排生产，才能使该厂月产值最大？月产值是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司招聘员工，指定三门考试课程，有两种考试方案．方案一：考试三门课程，至少有两门及格为考试通过；方案二：在三门课程中，随机选取两门，这两门都及格为考试通过．假设某应聘者对三门指定课程考试及格的概率分别是，，，且三门课程考试是否及格相互之间没有影响．

    （1）分别求该应聘者用方案一和方案二时考试通过的概率；

    （2）试比较该应聘者在上述两种方案下考试通过的概率的大小，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】把个不同的球随机地放入编号为1，2，…，的个盒子内，求1号盒恰有个球的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知曲线的参数方程为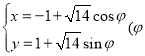为参数），以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为．曲线的极坐标方程为，曲线与曲线的交线为直线．

    （1）求直线和曲线的直角坐标方程；

    （2）直线与轴交于点，与曲线相交于，两点，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列满足条件：，且是公比为的等比数列，设.

    （1）求出使不等式成立的的取值范围；

    （2）求和，其中；

    （3）设，求数列的最大项和最小项的值.

    查看答案和解析>>

    同步练习册答案