
【题目】如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PB、PD与平面ABCD所成角的正切值依次是1、![]() ,AP=2,E、F依次是PB、PC的中点.
,AP=2,E、F依次是PB、PC的中点.

(1)求证:PB⊥平面AEFD;
(2)求直线EC与平面PAD所成角的正弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)由PA⊥平面ABCD,得AD⊥PA,结合AD⊥AB,得AD⊥平面PAB,从而AD⊥PB,由PB与平面ABCD所成角的正切值为1,可得AB=AP,最后根据△PAB中,中线AE⊥PB且AE、AD是平面AEFD内的相交直线,证出PB⊥平面AEFD;(2)根据PD与平面ABCD所成角的正切值是![]() ,即可求得AD,取PA中点G,CD中点H,连接EG、GH、GD,证明∠HGD即为直线EC与平面PAD所成的角,求出GH,即可求出直线EC与平面PAD所成角的正弦值.
,即可求得AD,取PA中点G,CD中点H,连接EG、GH、GD,证明∠HGD即为直线EC与平面PAD所成的角,求出GH,即可求出直线EC与平面PAD所成角的正弦值.
(1)证明:∵PA⊥平面ABCD,底面ABCD是矩形
∴AD⊥平面PAB,∴AD⊥PB 因为PA⊥平面ABCD,
故得到PD与平面ABCD所成角为角PBA,正切值为1,故得到AB=AP;
∵E是PB的中点,AB=AP,∴AE⊥PB
∵AB∩AE=A,
∴PB⊥平面AEFD
(2)因为PA⊥平面ABCD, PD与平面ABCD所成角的正切值是![]() ,即角PDA的正切值为
,即角PDA的正切值为![]() ,故得到
,故得到![]() 进而得到AD=4,
进而得到AD=4,
∵PA⊥平面ABCD,∴CD⊥PA,
又CD⊥AD,∴CD⊥平面PAD,
取PA中点G,CD中点H,连接EG、GH、GD,
则EG∥AB∥CD且![]() ,
,
∴EGHC是平行四边形,∴EC∥HG
∴∠HGD即为直线EC与平面PAD所成的角
在Rt△GAD中,![]()
![]() ,故得到
,故得到![]() ,
,![]() ,
,
∴直线EC与平面PAD所成角的正弦值为![]()


科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆![]() 的方程为
的方程为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)
为参数)
(1)求圆![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若直线![]() 与圆
与圆![]() 相切,求实数
相切,求实数![]() 的值;
的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|(x﹣2m+1)(x﹣m+2)<0},B={x|1≤x+1≤4}.
(1)若m=1,求A∩B;
(2)若A∩B=A,求实数m的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (α为参数)M是C1上的动点,P点满足
(α为参数)M是C1上的动点,P点满足 ![]() =2
=2 ![]() ,P点的轨迹为曲线C2
,P点的轨迹为曲线C2
(1)求C2的方程;
(2)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线θ= ![]() 与C1的异于极点的交点为A,与C2的异于极点的交点为B,求|AB|.
与C1的异于极点的交点为A,与C2的异于极点的交点为B,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过点
过点![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(1) 求圆![]() 的方程;
的方程;
(2)问是否存在满足以下两个条件的直线![]() :①斜率为
:①斜率为![]() ;②直线被圆
;②直线被圆![]() 截得的弦为
截得的弦为![]() ,以
,以![]() 为直径的圆过原点. 若存在这样的直线,请求出其方程;若不存在,请说明理由.
为直径的圆过原点. 若存在这样的直线,请求出其方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某交通要道以往的日车流量(单位:万辆)进行统计,得到如下记录:
日车流量x | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
频率 | 0.05 | 0.25 | 0.35 | 0.25 | 0.10 | 0 |
将日车流量落入各组的频率视为概率,并假设每天的车流量相互独立.
(1)求在未来连续3天里,有连续2天的日车流量都不低于10万辆且另1天的日车流量低于5万辆的概率;
(2)用X表示在未来3天时间里日车流量不低于10万辆的天数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
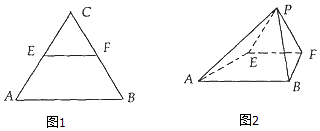
【题目】等腰△ABC中,AC=BC= ![]() ,AB=2,E,F分别为AC,BC的中点,将△EFC沿EF折起,使得C到P,得到四棱锥P﹣ABFE,且AP=BP=
,AB=2,E,F分别为AC,BC的中点,将△EFC沿EF折起,使得C到P,得到四棱锥P﹣ABFE,且AP=BP= ![]() .
. 
(1)求证:平面EFP⊥平面ABFE;
(2)求二面角B﹣AP﹣E的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com