
【题目】选修4 — 4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为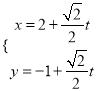 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ).
).
(1)分别写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盒子中装有四张大小形状均相同的卡片,卡片上分别标有数![]() 其中
其中![]() 是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
(1)求事件![]() “在一次试验中,得到的数为虚数”的概率
“在一次试验中,得到的数为虚数”的概率![]() 与事件
与事件![]() “在四次试验中,
“在四次试验中,
至少有两次得到虚数” 的概率![]() ;
;
(2)在两次试验中,记两次得到的数分别为![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当生物死亡后,它机体内原有的碳14会按确定的规律衰减.按照惯例,人们将每克组织的碳14含量作为一个单位大约每经过5730年,一个单位的碳14衰减为原来的一半,这个时间称为“半衰期”.当死亡生物组织内的碳14的含量不足死亡前的千分之一时,用一般的放射性探测器就测不到碳14了.如果用一般的放射性探测器不能测到碳14,那么死亡生物组织内的碳14至少经过了_____个“半衰期”.(提示:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的最大值为3,其图象相邻两条对称轴之间的距离为
的最大值为3,其图象相邻两条对称轴之间的距离为![]() .
.
(Ⅰ)求函数![]() 的解析式和当
的解析式和当![]() 时
时![]() 的单调减区间;
的单调减区间;
(Ⅱ)![]() 的图象向右平行移动
的图象向右平行移动![]() 个长度单位,再向下平移1个长度单位,得到
个长度单位,再向下平移1个长度单位,得到![]() 的图象,用“五点法”作出
的图象,用“五点法”作出![]() 在
在![]() 内的大致图象.
内的大致图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为
的棱长为![]() ,
, ![]() 分别是
分别是![]() 的中点,点
的中点,点![]() 在棱
在棱![]()
上, ![]() (
(![]() ).
).

(Ⅰ)三棱锥![]() 的体积分别为
的体积分别为![]() ,当
,当![]() 为何值时,
为何值时, ![]() 最大?最大值为多少?
最大?最大值为多少?
(Ⅱ)若![]() 平面
平面![]() ,证明:平面
,证明:平面![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,短轴长和焦距都等于2,
轴上,短轴长和焦距都等于2, ![]() 是椭圆上的一点,且
是椭圆上的一点,且![]() 在第一象限内,过
在第一象限内,过![]() 且斜率等于
且斜率等于![]() 的直线与椭圆
的直线与椭圆![]() 交于另一点
交于另一点![]() ,点
,点![]() 关于原点的对称点为
关于原点的对称点为![]() .
.

(Ⅰ)证明:直线![]() 的斜率为定值;
的斜率为定值;
(Ⅱ)求![]() 面积的最大值,并求此时直线
面积的最大值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究变量![]() ,
,![]() 得到一组样本数据,进行回归分析,有以下结论
得到一组样本数据,进行回归分析,有以下结论
①残差平方和越小的模型,拟合的效果越好;
②用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小说明拟合效果越好;
越小说明拟合效果越好;
③线性回归方程对应的直线![]() 至少经过其样本数据点中的一个点;
至少经过其样本数据点中的一个点;
④若变量![]() 和
和![]() 之间的相关系数为
之间的相关系数为![]() ,则变量
,则变量![]() 和
和![]() 之间的负相关很强.
之间的负相关很强.
以上正确说法的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com