练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】一辆单向行驶的汽车，满载为25人，全程共设14个车站，途中每个车站均可上下乘客，由不同的起点到达不同的终点的乘客应购买不同的车票，在一次单程行驶中，车上最多卖出不同的车票的个数是（ ）

    A.63B.65C.67D.69

    【答案】C

    【解析】

    根据汽车要卖最多种票，车上应准备每个车站到达后它后面每一个车站的车票，然后再以前面个车站中的每一个作为起点，后面个车站作为终点，求出车票数，再根据满载为25人，即可得出答案.

    上应准备每个车站到达后它后面每一个车站的车票，

    所以一共应准备（种），

    但不可能在一次单程行驶中都卖得出去，

    以前面个车站中的每一个作为起点，后面个车站作为终点，

    应当有（种），

    但持有这种票的乘客都要通过号车站与号车站之间，

    但由于汽车满员为25人，

    所以这种车票至少会有（种）卖不出去，

    所以车上最多卖出不同的车票的个数是（种）.

    故选：C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知两个不同的单位向量与之间满足关系：，其中．

    （1）若，求的解析式；

    （2）能否和垂直？能否和平行？若不能，则说明理由；若能，则求出对应的k值；

    （3）求与夹角的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正三棱锥的高为6，内切球（与四个面都相切）表面积为，则其底面边长为（ ）

    A. 18 B. 12 C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若函数在上是增函数，求实数的取值范围；

    （2）若函数在上的最小值为3，求实数的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为实数，函数.

    （1）若是函数的一个极值点，求实数的取值；

    （2）设，若，使得成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，直线的方程为，曲线：（为参数，），在以原点为极点，轴正半轴为极轴的极坐标系中，曲线：.

    （1）求曲线的普通方程和曲线的直角坐标方程；

    （2）若直线与曲线有公共点，且直线与曲线的交点恰好在曲线与轴围成的区域（不含边界）内，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-5：不等式选讲

    已知函数.

    （1）求不等式的解集；

    （2）若对恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

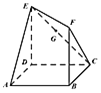
    【题目】如图，四边形ABCD是边长为1的正方形，平面ABCD，平面ABCD，且，G为线段EC上的动点，则下列结论中正确的是______

    ；该几何体外接球的表面积为；

    若G为EC中点，则平面AEF；

    的最小值为3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

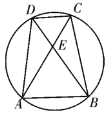
    【题目】如图，在圆内接等腰梯形中，已知，对角线、交于点，且图中各条线段长均为正整数，，圆的半径．

    （1）求证：图中存在一个三角形，其三边长均为质数且组成等差数列；

    （2）若给图中的线（包括圆、梯形、梯形的对角线）作点染色，使、、染上红色，其他点染上红蓝色之一，求证：图中存在三个同色点，两两距离相等且长度为质数．

    查看答案和解析>>

    同步练习册答案