练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    经过曲线C：(为参数)的中心作直线l:（t为参数）的垂线，求中心到垂足的距离.

    中心到垂足的距离为


    解析:

    由曲线C的参数方程

    消去参数，

    得(x-3)2+y2=9.

    曲线C表示以（3，0）为圆心，3为半径的圆.

    由直线l的参数方程,

    消去参数t,得y=x.

    表示经过原点，倾斜角为30°的直线.

    如图,在直角三角形OCD中，OC=3，∠COD=30°，

    所以CD=.所以中心到垂足的距离为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014届海南省高二上期末考试文科数学试卷（解析版） 题型：解答题

    已知曲线C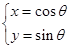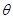：（为参数）.

    (1)将C的参数方程化为普通方程；

    (2)若把C上各点的坐标经过伸缩变换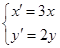后得到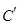曲线，求曲线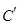上任意一点到两坐标轴距离之积的最大值．

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年辽宁省抚顺二中高三（上）第一次月考数学试卷（理科）（解析版） 题型：解答题

    选修4-4：坐标系与参数方程
    已知圆锥曲线C：（θ为参数）和定点，F1，F2是此圆锥曲线的左、右焦点．
    （1）以原点O为极点，以x轴的正半轴为极轴建立极坐标系，求直线AF2的极坐标方程；
    （2）经过点F1，且与直线AF2垂直的直线l交此圆锥曲线于M、N两点，求||MF1|-|NF1||的值．

    查看答案和解析>>

    科目：高中数学 来源：2011年辽宁省大连八中高考数学模拟试卷（文科）（解析版） 题型：解答题

    选修4-4：坐标系与参数方程
    已知圆锥曲线C：（θ为参数）和定点，F1，F2是此圆锥曲线的左、右焦点．
    （1）以原点O为极点，以x轴的正半轴为极轴建立极坐标系，求直线AF2的极坐标方程；
    （2）经过点F1，且与直线AF2垂直的直线l交此圆锥曲线于M、N两点，求||MF1|-|NF1||的值．

    查看答案和解析>>

    科目：高中数学 来源：2011年福建省福州三中高考数学六模试卷（理科）（解析版） 题型：解答题

    （1）选修4-4：矩阵与变换
    已知曲线C1：y=绕原点逆时针旋转45°后可得到曲线C2：y2-x2=2，
    （I）求由曲线C1变换到曲线C2对应的矩阵M1；    
    （II）若矩阵，求曲线C1依次经过矩阵M1，M2对应的变换T1，T2变换后得到的曲线方程．
    （2）选修4-4：坐标系与参数方程
    已知直线l的极坐标方程是ρcosθ+ρsinθ-1=0．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，在曲线C：（θ为参数）上求一点，使它到直线l的距离最小，并求出该点坐标和最小距离．
    （3）（选修4-5：不等式选讲）
    将12cm长的细铁线截成三条长度分别为a、b、c的线段，
    （I）求以a、b、c为长、宽、高的长方体的体积的最大值；
    （II）若这三条线段分别围成三个正三角形，求这三个正三角形面积和的最小值．

    查看答案和解析>>

    科目：高中数学 来源：2013年辽宁省大连八中高考适应性考试数学试卷（理科）（解析版） 题型：解答题

    选修4-4：坐标系与参数方程
    已知圆锥曲线C：（θ为参数）和定点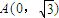，F1，F2是此圆锥曲线的左、右焦点．
    （1）以原点O为极点，以x轴的正半轴为极轴建立极坐标系，求直线AF2的极坐标方程；
    （2）经过点F1，且与直线AF2垂直的直线l交此圆锥曲线于M、N两点，求||MF1|-|NF1||的值．

    查看答案和解析>>

    同步练习册答案