
【题目】设函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集
的解集
(2)若函数![]() ,且
,且![]() 有解,求
有解,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
(1)当![]() 时,不等式化为|x+2|<x2,去绝对值,解不等式即可;
时,不等式化为|x+2|<x2,去绝对值,解不等式即可;
(2)求出g(x)的最小值,使得所以g(x)min≤11即可.
(1)当a=2时,不等式化为|x+2|<x2,
所以-x2<x+2<x2,所以x>2或x<-1,
所以不等式的解集为:{x|x>2或x<-1}.
(2)方法一:g(x)=f(2x)+f(1-x)
=|2x+a|+|x-(a+1)|=|x+![]() |+|x+
|+|x+![]() |+|x-(a+1)|
|+|x-(a+1)|
≥|![]() +a+1|=|
+a+1|=|![]() +1|,
+1|,
因为g(x)≤11(a>0)有解,所以g(x)min≤11,即![]() ,
,
所以3a≤20,所以0<a![]() ,
,
所以a的取值范围为(0,![]() ];
];
方法二: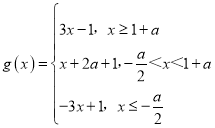 ,
,
当x=![]() 时,
时,![]() ,
,
因为g(x)≤11(a>0)有解,所以g(x)min≤11,即![]() ,
,
所以3a≤20,所以0<a![]() ,
,
所以a的取值范围为(0,![]() ].
].


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】下图是国家统计局今年4月11日发布的2018年3月到2019年3月全国居民消费价格的涨跌幅情况折线图.(注:2019年2月与2018年2月相比较称同比,2019年2月与2019年1月相比较称环比),根据该折线图,下列结论错误的是
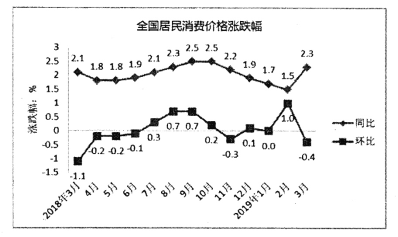
A. 2018年3月至2019年3月全国居民消费价格同比均上涨
B. 2018年3月至2019年3月全国居民消费价格环比有涨有跌
C. 2019年3月全国居民消费价格同比涨幅最大
D. 2019年3月全国居民消费价格环比变化最快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分
沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时。如图,某沙漏由上下两个圆锥组成,圆锥的底面直径和高均为8cm,细沙全部在上部时,其高度为圆锥高度的![]() (细管长度忽略不计).
(细管长度忽略不计).

(1)如果该沙漏每秒钟漏下0.02cm3的沙,则该沙漏的一个沙时为多少秒(精确到1秒)?
(2)细沙全部漏入下部后,恰好堆成个一盖住沙漏底部的圆锥形沙堆,求此锥形沙堆的高度(精确到0.1cm).
查看答案和解析>>
科目:高中数学 来源: 题型:
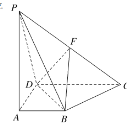
【题目】如图:四棱锥P-ABCD底面为一直角梯形,AB⊥AD,CD⊥AD,CD=2AB,PA⊥平面ABCD,F是PC中点。
(Ⅰ)求证:平面PDC⊥平面PAD;
(Ⅱ)求证:BF∥平面PAD。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科研人员在对人体脂肪含量和年龄之间关系的研究中,获得了一些年龄和脂肪含量的简单随机样本数据,如下表:
| 26 | 27 | 39 | 41 | 49 | 53 | 56 | 58 | 60 | 61 |
| 14.5 | 17.8 | 21.2 | 25.9 | 26.3 | 29.6 | 31.4 | 33.5 | 35.2 | 34.6 |
根据上表的数据得到如下的散点图.
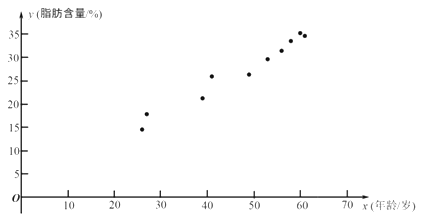
(1)根据上表中的样本数据及其散点图:
(i)求![]() ;
;
(i)计算样本相关系数(精确到0.01),并刻画它们的相关程度.
(2)若![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,求
,求![]() 的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量.
的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量.
附:参考数据:img src="http://thumb.zyjl.cn/Upload/2019/08/18/08/786210e5/SYS201908180802150104289801_ST/SYS201908180802150104289801_ST.007.png" width="51" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式:相关系数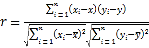
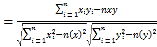
回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为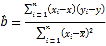 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
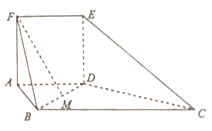
【题目】如图,在多面体![]() 中,平面
中,平面![]() 平面
平面![]() .四边形
.四边形![]() 为正方形,四边形
为正方形,四边形![]() 为梯形,且
为梯形,且![]() ,
,![]() 是边长为1的等边三角形,M为线段
是边长为1的等边三角形,M为线段![]() 中点,
中点,![]() .
.
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)线段![]() 上是否存在点N,使得直线
上是否存在点N,使得直线![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com