练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

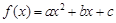    已知函数和函数，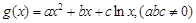

    （1）证明：只要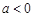，无论b取何值，函数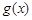在定义域内不可能总为增函数；

    （2）在同一函数图象上任意取不同两点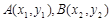，线段AB的中点为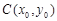，记直线AB的斜率为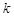，①对于函数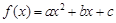，求证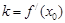：；②对于函数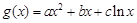，是否具有与①同样的性质？证明你的结论．

     

    【答案】

    证明：（1）若在上是增函数，则恒成立，从而必有在上恒成立。

    因为由二次函数的性质可知不可能恒成立，因此函数在定义域内不可能总为增函数。

    （2）①对于有，。又因为，所以成立。

    ②对于函数，不妨设，则。

    又因为，如果有①的性质，则，即有，化简得，也就是

    令，则。设，则，所以在上单调递增，，故不可能成立，从而不成立，因此函数不具有与①同样的性质。

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f(x)=x
    1
    2
    ，g(x)=(
    1
    2
    )x    ，则在[0，+∞）上（　　）
    A、f（x）和g（x）都是增函数
    B、f（x）是减函数，g（x）是增函数
    C、f（x）和g（x）都是减函数
    D、f（x）是增函数，g（x）是减函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=x2（x-a），其中a∈R．g（x）=f（x）+f'（x）．
    （I）当函数f（x）的图象在点（1，f（1））处的切线斜率为2时，求此直线在y轴上的截距；
    （II）求证：g（x）既有极大值又有极小值；
    （III）若g（x）取极大值和极小值对应的x值分别在区间（-2，-1）和（3，4）内，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

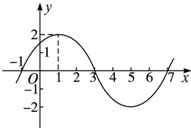    （2013•东城区模拟）已知函数f（x）=Asin（ω+φ）（A＞0，ω＞0，|φ|＜
    π
    2
    ）的图象的一部分如图所示．
    （Ⅰ）求函数f（x）的解析式；
    （Ⅱ）求函数y=f（x）+2cos（
    π
    4
    x+
    π
    4
    ）（x∈[-6，-
    2
    3
    ]）的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2008•武汉模拟）已知函数和函数f（x）=ax3-x2+1（a为常数）
    （1）当a＞0时，求函数f（x）的单调递减区间；
    （2）若方程f（x）=0有三个不同的解，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年底江苏省连云港市赣榆高级中学高三（下）摸底数学试卷（解析版） 题型：解答题

    已知函数和函数g（x）=lnx，记F（x）=f（x）+g（x）．
    （1）当时，若f（x）在[1，2]上的最大值是f（2），求实数a的取值范围；
    （2）当a=1时，判断F（x）在其定义域内是否有极值，并予以证明；
    （3）对任意的，若F（x）在其定义域内既有极大值又有极小值，试求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案