
设![]() 、
、![]() 为坐标平面
为坐标平面![]() 上的点,直线
上的点,直线![]() (
(![]() 为坐标原点)与抛物线
为坐标原点)与抛物线![]() 交于点
交于点![]() (异于
(异于![]() ).
).
(1) 若对任意![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,试问当
上,试问当![]() 为何值时,点
为何值时,点![]() 在某一圆上,并求出该圆方程
在某一圆上,并求出该圆方程![]() ;
;
(2) 若点![]() 在椭圆
在椭圆![]() 上,试问:点
上,试问:点![]() 能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
(3) 对(1)中点![]() 所在圆方程
所在圆方程![]() ,设
,设![]() 、
、![]() 是圆
是圆![]() 上两点,且满足
上两点,且满足![]() ,试问:是否存在一个定圆
,试问:是否存在一个定圆![]() ,使直线
,使直线![]() 恒与圆
恒与圆![]() 相切. k*s*5*u
相切. k*s*5*u
解:(1)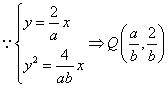 ,-----------------------------------------------------2分
,-----------------------------------------------------2分
代入![]()
![]() ---------------------------------- 4分
---------------------------------- 4分
当![]() 时,点
时,点 ![]() 在圆
在圆![]()
![]() 上-------------------------------------------5分
上-------------------------------------------5分
(2)![]() 在椭圆
在椭圆![]() 上,即
上,即![]()
![]()
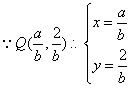
![]() 点
点![]() 在双曲线
在双曲线![]() 上--------------------------------------------------------------------10分
上--------------------------------------------------------------------10分
(3)![]() 圆
圆![]() 的方程为
的方程为![]()
设![]() 由
由![]()
![]()
![]()
![]() ----------------------------------------------------------------------------------------------12分
----------------------------------------------------------------------------------------------12分
又
![]() ,
,![]() ------------14分
------------14分
又原点![]() 到直线
到直线![]() 距离
距离![]()
![]() ,即原点
,即原点![]() 到直线
到直线![]() 的距离恒为
的距离恒为![]()
![]() 直线
直线![]() 恒与圆
恒与圆![]() 相切。---------------------------------------------------------15分
相切。---------------------------------------------------------15分


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:
(本题满分16分;第(1)小题5分,第(2)小题5分,第(3)小题6分)
设![]() 、
、![]() 为坐标平面
为坐标平面![]() 上的点,直线
上的点,直线![]() (
(![]() 为坐标原点)与抛物线
为坐标原点)与抛物线![]() 交于点
交于点![]() (异于
(异于![]() ).
).
若对任意![]()
![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,试问当
上,试问当![]() 为何值时,点
为何值时,点![]() 在某一圆上,并求出该圆方程
在某一圆上,并求出该圆方程![]() ;
;
若点![]() 在椭圆
在椭圆![]() 上,试问:点
上,试问:点![]() 能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
对(1)中点![]() 所在圆方程
所在圆方程![]() ,设
,设![]() 、
、![]() 是圆
是圆![]() 上两点,且满足
上两点,且满足![]() ,试问:是否存在一个定圆
,试问:是否存在一个定圆![]() ,使直线
,使直线![]() 恒与圆
恒与圆![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源:2013届江苏南京学大教育专修学校高二五月理科数学试卷(解析版) 题型:填空题
设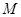 是把坐标平面上的点的横坐标伸长为原来的4倍,纵坐标伸长为原来的3倍的伸压变换,则圆
是把坐标平面上的点的横坐标伸长为原来的4倍,纵坐标伸长为原来的3倍的伸压变换,则圆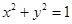 在
在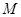 的作用下的新曲线的方程是
的作用下的新曲线的方程是
查看答案和解析>>
科目:高中数学 来源:2010年上海市徐汇区高三第二次模拟考试数学卷(理) 题型:解答题
(本题满分16分;第(1)小题5分,第(2)小题5分,第(3)小题6分)
设 、
、 为坐标平面
为坐标平面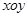 上的点,直线
上的点,直线 (
( 为坐标原点)与抛物线
为坐标原点)与抛物线 交于点
交于点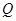 (异于
(异于 ).
).
(1)
若对任意 ,点
,点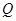 在抛物线
在抛物线 上,试问当
上,试问当 为何值时,点
为何值时,点 在某一圆上,并求出该圆方程
在某一圆上,并求出该圆方程 ;
;
(2)
若点 在椭圆
在椭圆 上,试问:点
上,试问:点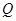 能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
(3)
对(1)中点 所在圆方程
所在圆方程 ,设
,设 、
、 是圆
是圆 上两点,且满足
上两点,且满足 ,试问:是否存在一个定圆
,试问:是否存在一个定圆 ,使直线
,使直线 恒与圆
恒与圆 相切.
相切.
查看答案和解析>>
科目:高中数学 来源:2011届永春一中、培元中学、季延中学和石光华侨联中高三第一次统考数 题型:解答题
本题有(1)、(2)、(3)三个选考题,每题7份,请考生任选2题作答,满分14分.
如果多做,则按所做的前两题计分.
选修4系列(本小题满分14分)
(1)(本小题满分7分)选修4-2:矩阵与变换
设 是把坐标平面上的点的横坐标伸长到
是把坐标平面上的点的横坐标伸长到 倍,纵坐标伸长到
倍,纵坐标伸长到 倍的伸压变换.
倍的伸压变换.
(Ⅰ)求矩阵 的特征值及相应的特征向量;
的特征值及相应的特征向量;
(Ⅱ)求逆矩阵 以及椭圆
以及椭圆 在
在 的作用下的新曲线的方程.
的作用下的新曲线的方程.
(2) (本小题满分7分)选修4-4:坐标系与参数方程
直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知直线l的极坐标方程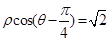 ,曲线C的参数方程为
,曲线C的参数方程为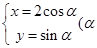 为参数),求曲线C截直线l所得的弦长
为参数),求曲线C截直线l所得的弦长
(3)(本小题满分7分)选修4—5:不等式选讲
已知 ,且
,且 、
、 、
、 是正数,求证:
是正数,求证: .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com