
【题目】已知双曲线![]() 的两条渐近线分别为直线
的两条渐近线分别为直线![]() ,
,![]() ,经过右焦点
,经过右焦点![]() 且垂直于
且垂直于![]() 的直线
的直线![]() 分别交
分别交![]() ,
,![]() 于
于![]() 两点,若
两点,若![]() ,
,![]() ,
,![]() 成等差数列,且
成等差数列,且![]() ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
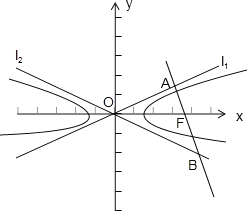
由双曲线的性质可得:|AF|=b,|OA|=a,∴tan∠AOF=![]() ,∴tan∠AOB=tan2∠AOF=
,∴tan∠AOB=tan2∠AOF=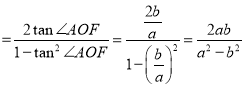 ,在直角三角形OAB中求出|AB|和|OB|,再根据等差中项列等式可得 a=2b,可得离心率.
,在直角三角形OAB中求出|AB|和|OB|,再根据等差中项列等式可得 a=2b,可得离心率.
由双曲线的性质可得:|AF|=b,|OA|=a,tan∠AOF=![]() ,
,
∴tan∠AOB=tan2∠AOF=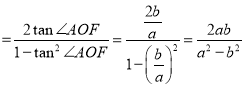
在Rt△OAB中,tan∠AOB=![]()
∴|OB|=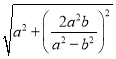 ,又|OA|,|AB|,|OB|成等差数列,∴2|AB|=|OA|+|OB|,
,又|OA|,|AB|,|OB|成等差数列,∴2|AB|=|OA|+|OB|,
∴ ,化简得:2a2﹣3ab﹣2b2=0,即(2a+b)(a﹣2b)=0,
,化简得:2a2﹣3ab﹣2b2=0,即(2a+b)(a﹣2b)=0,
∴a﹣2b=0,即a=2b,∴a2=4b2=4(c2﹣a2),5a2=4c2,∴e2=![]() .
.
故选:A.


科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,圆
中,圆![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 分别与圆
分别与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.

(Ⅰ)若![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
(Ⅱ)若直线![]() 过点
过点![]() ,证明:
,证明:![]() 为定值,并求此定值.
为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校研究性学习小组发现,学生上课的注意力指标随着听课时间的变化而变化.老师讲课开始时学生的兴趣激增,接下来学生的兴趣将保持较理想的状态一段时间,随后学生的注意力开始分散.该小组发现注意力指标![]() 与上课时刻第
与上课时刻第![]() 分钟末的关系如下(
分钟末的关系如下(![]() ,设上课开始时,t=0):
,设上课开始时,t=0): .若上课后第5分钟末时的注意力指标为140.
.若上课后第5分钟末时的注意力指标为140.
(1)求![]() 的值;
的值;
(2)上课后第5分钟末和第35分钟末比较,哪个时刻注意力更集中?
(3)在一节课中,学生的注意力指标至少达到140的时间能保持多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项的和为
项的和为![]() ,且
,且![]() ,
,![]() .
.
(1)证明数列![]() 为等比数列,并求出数列
为等比数列,并求出数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项的和
项的和![]() ;
;
(3)设函数![]() (
(![]() 为常数),且(2)中的
为常数),且(2)中的![]() >
>![]() 对任意的
对任意的![]() 和
和![]() 都成立,求实数
都成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 的圆心,
的圆心, ![]() 是圆上的动点,点
是圆上的动点,点![]() 在圆的半径
在圆的半径![]() 上,且有点
上,且有点![]() 和
和![]() 上的点
上的点![]() ,满足
,满足![]() ,
, ![]() .
.
(1)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)若斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 相切,直线
相切,直线![]() 与(1)中所求点
与(1)中所求点![]() 的轨迹交于不同的两点
的轨迹交于不同的两点![]() ,
, ![]() ,
, ![]() 是坐标原点,且
是坐标原点,且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
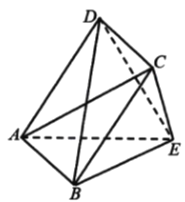
【题目】如图,在多面体![]() 中,
中,![]() 和
和![]() 交于一点,除
交于一点,除![]() 以外的其余各棱长均为2.
以外的其余各棱长均为2.
![]() 作平面
作平面![]() 与平面
与平面![]() 的交线
的交线![]() ,并写出作法及理由;
,并写出作法及理由;
![]() 求证:平面
求证:平面![]() 平面
平面![]() ;
;
![]() 若多面体的体积为2,求直线
若多面体的体积为2,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com