
【题目】设![]() ,其中
,其中![]() .
.
(1)当q=1时,化简:![]() ;
;
(2)当q=n时,记![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
【答案】(1)![]() (2) 当n=1,2时,
(2) 当n=1,2时,![]() ;当
;当![]() 时,
时,![]()
【解析】
(1) 当q=1时,![]() ,从而得到结果;
,从而得到结果;
(2) 当q=n时,由二项式定理可得![]() ,猜想、归纳,用数学归纳法加以证明即可.
,猜想、归纳,用数学归纳法加以证明即可.
(1)当q=1时,![]() ,
,
由于
![]() ,
,
其中![]() .
.
所以原式![]()
(2)【解法一】当q=n时,![]() ,
,
所以![]() ,所以
,所以![]() ,
,
令x=1,得![]() ,
,
当n=1,2时,![]() ;当
;当![]() 时,
时,![]() ,即
,即![]() .
.
下面先用数学归纳法证明:当![]() 时,
时,![]() ,……(☆)
,……(☆)
①当n=3时,![]() ,(☆)式成立;
,(☆)式成立;
②设![]() 时,(☆)式成立,即
时,(☆)式成立,即![]() ,
,
则![]() 时,(☆)式右边
时,(☆)式右边![]()
![]() .
.
这就是说,当![]() ,(☆)式也成立.
,(☆)式也成立.
综合①②知,当![]() 时,
时,![]() .
.
所以,当n=1,2时,![]() ;当
;当![]() 时,
时,![]()
【解法二】
当q=n时,![]() ,
,
所以![]() ,所以
,所以![]() ,
,
令x=1,得![]() ,.
,.
要比较![]() 与
与![]() 的大小,即可比较
的大小,即可比较![]() 与
与![]() 的大小,
的大小,
设![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 上递增,
上递增,
由![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 上递减,
上递减,
所以当n=1,2时,![]() ,
,![]()
当![]() 时,
时,![]() ,即
,即![]() ,
,
即![]() ,即
,即![]() ,
,
综上所述,当n=1,2时,![]() ;当
;当![]() 时,
时,![]() .
.
【解法三】
当q=n时,![]() ,
,
所以![]() ,所以
,所以![]() ,
,
令x=1,得![]() ,
,
当n=1,2时,![]() ;当
;当![]() 时,
时,![]() .
.
下面用数学归纳法证明:![]() ,
,![]() ,
,![]() ,……(*)
,……(*)
①当n=3时,![]() ,因为
,因为![]() ,所以(*)式成立;
,所以(*)式成立;
②设![]() 时,(*)式成立,即有
时,(*)式成立,即有![]() ,
,
所以![]() (因为
(因为![]() ).
).
又因为![]() ,即
,即![]() ,
,
所以![]() ,
,
即![]() ,所以,当
,所以,当![]() 时,(*)式也成立.
时,(*)式也成立.
综合①②,对任何![]() ,
,![]() 都成立.
都成立.
所以,当n=1,2时,![]() ;当
;当![]() 时,
时,![]() .
.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】用“算筹”表示数是我国古代计数方法之一,计数形式有纵式和横式两种,如图1所示.金元时期的数学家李治在《测圆海镜》中记载:用“天元术”列方程,就是用算筹来表示方程中各项的系数.所谓“天元术”,即是一种用数学符号列方程的方法,“立天元一为某某”,意即“设![]() 为某某”.如图2所示的天元式表示方程
为某某”.如图2所示的天元式表示方程![]() ,其中
,其中![]() 表示方程各项的系数,均为筹算数码,在常数项旁边记一“太”字或在一次项旁边记一“元”字,“太”或“元”向上每层减少一次幂,向下每层增加一次幂.试根据上述数学史料,判断图3所示的天元式表示的方程是________________
表示方程各项的系数,均为筹算数码,在常数项旁边记一“太”字或在一次项旁边记一“元”字,“太”或“元”向上每层减少一次幂,向下每层增加一次幂.试根据上述数学史料,判断图3所示的天元式表示的方程是________________

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某媒体为调查喜爱娱乐节目![]() 是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
喜欢节目A | 不喜欢节目A | 总计 | |
男性观众 | |||
女性观众 | |||
总计 |
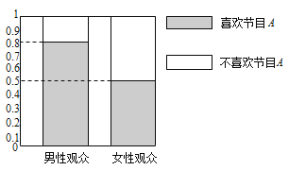
(1)根据该等高条形图,完成右上![]() 列联表,并用独立性检验的方法分析,则在犯错误的概率不超过多少的前提下认为喜欢娱乐节目
列联表,并用独立性检验的方法分析,则在犯错误的概率不超过多少的前提下认为喜欢娱乐节目![]() 与观众性别有关?
与观众性别有关?
(2)从男性观众中按喜欢节目![]() 与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目
与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目![]() 和1名不喜欢节目
和1名不喜欢节目![]() 的概率.
的概率.
附: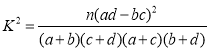
| 0.100 | 0.050 | 0.010 | 0.00 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某公园内有一块矩形绿地区域ABCD,已知AB=100米,BC=80米,以AD,BC为直径的两个半圆内种植花草,其它区域种值苗木. 现决定在绿地区域内修建由直路BN,MN和弧形路MD三部分组成的观赏道路,其中直路MN与绿地区域边界AB平行,直路为水泥路面,其工程造价为每米2a元,弧形路为鹅卵石路面,其工程造价为每米3a元,修建的总造价为W元. 设![]() .
.
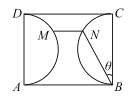
(1)求W关于![]() 的函数关系式;
的函数关系式;
(2)如何修建道路,可使修建的总造价最少?并求最少总造价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格,某校有800名学生参加了初赛,所有学生的成绩均在区间![]() 内,其频率分布直方图如图.
内,其频率分布直方图如图.

(Ⅰ)求获得复赛资格的人数;
(Ⅱ)从初赛得分在区间![]() 的参赛者中,利用分层抽样的方法随机抽取
的参赛者中,利用分层抽样的方法随机抽取![]() 人参加学校座谈交流,那么从得分在区间
人参加学校座谈交流,那么从得分在区间![]() 与
与![]() 各抽取多少人?
各抽取多少人?
(Ⅲ)从(Ⅱ)抽取的![]() 人中,选出
人中,选出![]() 人参加全市座谈交流,设
人参加全市座谈交流,设![]() 表示得分在区间
表示得分在区间![]() 中参加全市座谈交流的人数,求
中参加全市座谈交流的人数,求![]() 的分布列及数学期望E(X).
的分布列及数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着移动支付的普及,中国人的生活方式正悄然巨变,带智能手机,不带钱包出门还渐成为中国人的新习惯![]() 年我国移动支付增长迅猛,据统计,某支付平台2017年移动支付的笔数占总支付笔数的
年我国移动支付增长迅猛,据统计,某支付平台2017年移动支付的笔数占总支付笔数的![]() .
.
![]() Ⅰ
Ⅰ![]() 从该支付平台2017年的所有支付中任取10笔,求移动支付笔数的期望和方差;
从该支付平台2017年的所有支付中任取10笔,求移动支付笔数的期望和方差;
![]() Ⅱ
Ⅱ![]() 现有500名使用该支付平台的用户,其中300名是城市用户,200名是农村用户,调查他们2017年个人移动支付的比例是否达到了
现有500名使用该支付平台的用户,其中300名是城市用户,200名是农村用户,调查他们2017年个人移动支付的比例是否达到了![]() ,得到
,得到![]() 列联表如下:
列联表如下:
个人移动支付达到了 | 个人移动支付达到了 | 合计 | |
城市用户 | 270 | 30 | 300 |
农村用户 | 170 | 30 | 200 |
合计 | 440 | 60 | 500 |
根据上表数据,问是否有![]() 的把握认为2017年个人移动支付比例达到了
的把握认为2017年个人移动支付比例达到了![]() 与该用户是城市用户还是农村用户有关?
与该用户是城市用户还是农村用户有关?
附:![]()
|
|
|
k |
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某企业中随机抽取了5名员工测试他们的艺术爱好指数![]() 和创新灵感指数
和创新灵感指数![]() ,统计结果如下表(注:指数值越高素质越优秀):
,统计结果如下表(注:指数值越高素质越优秀):
![]()
(1)求创新灵感指数![]() 关于艺术爱好指数
关于艺术爱好指数![]() 的线性回归方程;
的线性回归方程;
(2)企业为提高员工的艺术爱好指数,要求员工选择音乐和绘画中的一种进行培训,培训音乐次数![]() 对艺术爱好指数
对艺术爱好指数![]() 的提高量为
的提高量为 ,培训绘画次数
,培训绘画次数![]() 对艺术爱好指数
对艺术爱好指数![]() 的提高量为
的提高量为![]() ,其中
,其中![]() 为参加培训的某员工已达到的艺术爱好指数.艺术爱好指数已达到3的员工甲选择参加音乐培训,艺术爱好指数已达到4的员工乙选择参加绘画培训,在他们都培训了20次后,估计谁的创新灵感指数更高?
为参加培训的某员工已达到的艺术爱好指数.艺术爱好指数已达到3的员工甲选择参加音乐培训,艺术爱好指数已达到4的员工乙选择参加绘画培训,在他们都培训了20次后,估计谁的创新灵感指数更高?
参考公式:回归方程![]() 中,
中, ,
,![]() .
.
参考数据:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com