
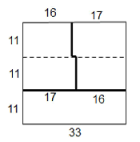
【题目】如图所示,将![]() 方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )
方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )
A.33B.56C.64D.78
【答案】B
【解析】
记分隔边的条数为![]() ,首先将方格按照按图分三个区域,分别染成三种颜色,粗线上均为分隔边,将方格的行从上至下依次记为
,首先将方格按照按图分三个区域,分别染成三种颜色,粗线上均为分隔边,将方格的行从上至下依次记为![]() ,列从左至右依次记为
,列从左至右依次记为![]() ,行
,行![]() 中方格出现的颜色数记为
中方格出现的颜色数记为![]() ,列
,列![]() 中方格出现的颜色个数记为
中方格出现的颜色个数记为![]() ,三种颜色分别记为
,三种颜色分别记为![]() ,对于一种颜色
,对于一种颜色![]() ,设
,设![]() 为含有
为含有![]() 色方格的行数与列数之和,定义当
色方格的行数与列数之和,定义当![]() 行含有
行含有![]() 色方格时,
色方格时,![]() ,否则
,否则![]() ,类似的定义
,类似的定义![]() ,计算得到
,计算得到![]() ,再证明
,再证明![]() ,再证明对任意
,再证明对任意![]() 均有
均有![]() ,最后求出分隔边条数的最小值.
,最后求出分隔边条数的最小值.
记分隔边的条数为![]() ,首先将方格按照按图分三个区域,分别染成三种颜色,粗线上均为分隔边,
,首先将方格按照按图分三个区域,分别染成三种颜色,粗线上均为分隔边,
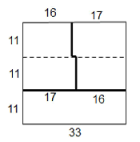
此时共有56条分隔边,即![]() ,
,
其次证明:![]() ,
,
将将方格的行从上至下依次记为![]() ,列从左至右依次记为
,列从左至右依次记为![]() ,行
,行![]() 中方格出现的颜色数记为
中方格出现的颜色数记为![]() ,列
,列![]() 中方格出现的颜色个数记为
中方格出现的颜色个数记为![]() ,三种颜色分别记为
,三种颜色分别记为![]() ,对于一种颜色
,对于一种颜色![]() ,设
,设![]() 为含有
为含有![]() 色方格的行数与列数之和,定义当
色方格的行数与列数之和,定义当![]() 行含有
行含有![]() 色方格时,
色方格时,![]() ,否则
,否则![]() ,类似的定义
,类似的定义![]() ,
,
所以![]() ,
,
由于染![]() 色的格有
色的格有![]() 个,设含有
个,设含有![]() 色方格的行有
色方格的行有![]() 个,列有
个,列有![]() 个,则
个,则![]() 色的方格一定再这个
色的方格一定再这个![]() 行和
行和![]() 列的交叉方格中,
列的交叉方格中,
从而![]() ,
,
所以![]() ①,
①,
由于在行![]() 中有
中有![]() 种颜色的方格,于是至少有
种颜色的方格,于是至少有![]() 条分隔边,
条分隔边,
类似的,在列![]() 中有
中有![]() 种颜色的方格,于是至少有
种颜色的方格,于是至少有![]() 条分隔边,
条分隔边,
则![]() ②
②
![]() ③
③
下面分两种情形讨论,
(1)有一行或一列所有方格同色,
不妨设有一行均为![]() 色,则方格的33列均含有
色,则方格的33列均含有![]() 的方格,又
的方格,又![]() 色的方格有363个,故至少有11行有
色的方格有363个,故至少有11行有![]() 色方格,于是
色方格,于是![]() ④
④
由①③④得
![]() ,
,
(2)没有一行也没有一列的所有方格同色,
则对任意![]() 均有
均有![]() ,
,
从而,由式②知:
![]() ,
,
综上,分隔边条数的最小值为56.
故选:B.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
【题目】有一种叫“对对碰”的游戏,游戏规则如下:一轮比赛中,甲乙两人依次轮流抛一枚质地均匀的硬币,甲先抛,每人抛3次,得分规则如下:甲第一次抛得![]() 分,再由乙第一次抛,若出现朝上的情况与甲第一次抛的朝上的情况一样,则本次得2分,否则得1分;再甲第二次抛,若出现朝上的情况与乙第一次抛的朝上的情况一样,则本次得分是乙第一次得分的基础上加1分,否则得1分;再乙第二次抛,若出现朝上的情况与甲第二次抛的朝上的情况一样,则本次得分是甲第二次得分的基础上加1分,否则得1分;按此规则,直到游戏结束.记甲乙累计得分分别为
分,再由乙第一次抛,若出现朝上的情况与甲第一次抛的朝上的情况一样,则本次得2分,否则得1分;再甲第二次抛,若出现朝上的情况与乙第一次抛的朝上的情况一样,则本次得分是乙第一次得分的基础上加1分,否则得1分;再乙第二次抛,若出现朝上的情况与甲第二次抛的朝上的情况一样,则本次得分是甲第二次得分的基础上加1分,否则得1分;按此规则,直到游戏结束.记甲乙累计得分分别为![]() .
.
(1)一轮游戏后,求![]() 的概率;
的概率;
(2)一轮游戏后,经计算得乙的数学期望![]() ,要使得甲的数学期望
,要使得甲的数学期望![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,AP,AB,AD两两垂直,BC∥AD,且AP=AB=AD=4,BC=2.
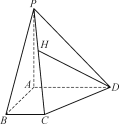
(1)求二面角P-CD-A的余弦值;
(2)已知H为线段PC上异于C的点,且DC=DH,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】蔬菜批发市场销售某种蔬菜,在一个销售周期内,每售出1吨该蔬菜获利500元,未售出的蔬菜低价处理,每吨亏损100元.统计该蔬菜以往100个销售周期的市场需求量,绘制下图所示频率分布直方图.
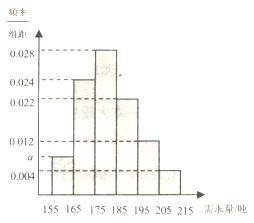
(Ⅰ)求![]() 的值,并求100个销售周期的平均市场需求量(以各组的区间中点值代表该组的数值);
的值,并求100个销售周期的平均市场需求量(以各组的区间中点值代表该组的数值);
(Ⅱ)若经销商在下个销售周期购进了190吨该蔬菜,设![]() 为该销售周期的利润(单位:元),
为该销售周期的利润(单位:元),![]() 为该销售周期的市场需求量(单位:吨).求
为该销售周期的市场需求量(单位:吨).求![]() 与
与![]() 的函数解析式,并估计销售的利润不少于86000元的概率.
的函数解析式,并估计销售的利润不少于86000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的右焦点为F,左顶点为A,离心率
)的右焦点为F,左顶点为A,离心率![]() ,且经过圆O:
,且经过圆O:![]() 的圆心.过点F作不与坐标轴重合的直线
的圆心.过点F作不与坐标轴重合的直线![]() 和该椭圆交于MN两点,且直线
和该椭圆交于MN两点,且直线![]()
![]() 分别与直线
分别与直线![]() 交于PQ两点.
交于PQ两点.
(1)求椭圆的方程;
(2)证明:![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),把曲线
为参数),把曲线![]() 横坐标缩短为原来的
横坐标缩短为原来的![]() ,纵坐标缩短为原来的一半,得到曲线
,纵坐标缩短为原来的一半,得到曲线![]() ,直线
,直线![]() 的普通方程是
的普通方程是![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系;
轴正半轴为极轴建立极坐标系;
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)记射线![]() 与
与![]() 交于点
交于点![]() ,与
,与![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com