
【题目】下列结论中正确的是( )
A.半圆弧以其直径为轴旋转一周所形成的曲面叫做球
B.直角三角形绕一直角边为轴旋转一周得到的旋转体是圆锥
C.夹在圆柱的两个平行截面间的几何体还是一个旋转体
D.用一个平面截圆锥底面与截面组成的部分是圆台
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 是各项均不为
是各项均不为![]() 的等差数列,公差为
的等差数列,公差为![]() ,
,![]() 为其前
为其前![]() 项和,且满足
项和,且满足
![]() ,
,![]() .数列
.数列![]() 满足
满足![]() ,
,![]() 为数列
为数列![]() 的前n项和.
的前n项和.
(1)求![]() 、
、![]() 和
和![]() ;
;
(2)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面上的一列点![]() 简记为
简记为![]() ,若由
,若由![]() 构成的数列
构成的数列![]() 满足
满足![]() ,(其中
,(其中![]() 是与
是与![]() 轴正方向相同的单位向量),则称
轴正方向相同的单位向量),则称![]() 为“
为“![]() 点列”.
点列”.
(1)试判断:![]() ,...是否为“
,...是否为“![]() 点列”?并说明理由.
点列”?并说明理由.
(2)若![]() 为“
为“![]() 点列”,且点
点列”,且点![]() 在点
在点![]() 的右上方.任取其中连续三点
的右上方.任取其中连续三点![]() ,判断
,判断![]() 的形状(锐角,直角,钝角三角形),并证明.
的形状(锐角,直角,钝角三角形),并证明.
(3)若![]() 为“
为“![]() 点列”,正整数
点列”,正整数![]() 满足:
满足:![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园举办雕塑展览吸引着四方宾客,旅游人数![]() 与人均消费
与人均消费![]() (元)的关系如下:
(元)的关系如下: .
.
(1)若游客客源充足,那么当天接待游客多少人时,公园的旅游收入最多?
(2)若公园每天运营成本为5万元(不含工作人员的工资),还要上缴占旅游收入![]() 的税收,其余自负盈亏,目前公园的工作人员维持在40人,要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内?(注:旅游收入=旅游人数×人均消费)
的税收,其余自负盈亏,目前公园的工作人员维持在40人,要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内?(注:旅游收入=旅游人数×人均消费)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
分数段 |
|
|
|
|
| 1∶1 | 2∶1 | 3∶4 | 4∶5 |

(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(![]() )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数(![]() )之比如下表所示,求数学成绩在
)之比如下表所示,求数学成绩在![]() 之外的人数.
之外的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,过椭圆的左焦点
,过椭圆的左焦点![]() 且倾斜角为
且倾斜角为![]() 的直线与圆
的直线与圆![]() 相交所得弦长为
相交所得弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,若存在,求直线
,若存在,求直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
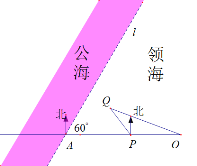
【题目】某海警基地码头![]() 的正西方向
的正西方向![]() 海里处有海礁界碑
海里处有海礁界碑![]() ,过点
,过点![]() 且与
且与![]() 成
成![]() 角(即北偏东
角(即北偏东![]() )的直线
)的直线![]() 为此处的一段领海与公海的分界线(如图所示)。在码头
为此处的一段领海与公海的分界线(如图所示)。在码头![]() 的正西方向且距离
的正西方向且距离![]() 点
点![]() 海里的领海海面
海里的领海海面![]() 处有一艘可疑船停留,基地指挥部决定在测定可疑船的行驶方向后,海警巡逻艇从
处有一艘可疑船停留,基地指挥部决定在测定可疑船的行驶方向后,海警巡逻艇从![]() 处即刻出发。若巡逻艇以可疑船的航速的
处即刻出发。若巡逻艇以可疑船的航速的![]() 倍
倍![]() 前去拦截,假定巡逻艇和可疑船在拦截过程中均未改变航向航速,将在点
前去拦截,假定巡逻艇和可疑船在拦截过程中均未改变航向航速,将在点![]() 处截获可疑船。
处截获可疑船。
(1)若可疑船的航速为![]() 海里
海里![]() 小时,
小时,![]() ,且可疑船沿北偏西
,且可疑船沿北偏西![]() 的方向朝公海逃跑,求巡逻艇成功拦截可疑船所用的时间。
的方向朝公海逃跑,求巡逻艇成功拦截可疑船所用的时间。
(2)若要确保在领海内(包括分界线)成功拦截可疑船,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有![]() 四个景点,一位游客来该市游览,已知该游客游览
四个景点,一位游客来该市游览,已知该游客游览![]() 的概率为
的概率为![]() ,游览
,游览![]() 、
、![]() 和
和![]() 的概率都是
的概率都是![]() ,且该游客是否游览这四个景点相互独立.
,且该游客是否游览这四个景点相互独立.
(1)求该游客至多游览一个景点的概率;
(2)用随机变量![]() 表示该游客游览的景点的个数,求
表示该游客游览的景点的个数,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】光农业科学研究所对冬季昼夜温差大小与反季节土豆发芽多少之间的关系进行分析研究,他们分别记录了11月1日至11月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如表资料:
日期 | 11月1日 | 11月2日 | 11月3日 | 11月4日 | 11月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 26 | 32 | 26 | 16 |
设农科所确定的研究方案是:先从这5组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是11月1日与11月5日的两组数据,请根据11月2日至11月4日的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过1颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
(注: 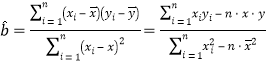 ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com