【题目】近期中央电视台播出的《中国诗词大会》火遍全国，下面是组委会在选拔赛时随机抽取的100名选手的成绩，按成绩分组，得到的频率分布表如下所示.
题号 | 分组 | 频数 | 频率 |
第1组 |
| 0.100 | |
第2组 |
| ① | |
第3组 |
| 20 | ② |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
第6组 |
| 100 | 1.00 |
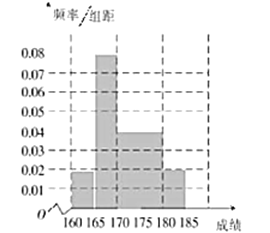
（1）请先求出频率分布表中①、②位置的相应数据，再完成如下的频率分布直方图；
（2）组委会决定在5名（其中第3组2名，第4组2名，第5组1名）选手中随机抽取2名选接受
考官进行面试，求第4组至少有1名选手被考官面试的概率.
【答案】（1）见解析；（2）
【解析】
（1）第1组的频数为人
，所以①处应填的数为
，从而第2组的频数为
，因此②处应填的数为
，即可得到答案。
（2）设第3组的2名选手为
，第4组的2名选手为
，第5组的1名选手为
，利用列举法得到基本事件的总数，再利用古典概型及其概率的计算公式，即可求解。
（1）第1组的频数为人，所以①处应填的数为
，从而第2组的频数为
，因此②处应填的数为
.
频率分布直方图如图所示，
（2）设第3组的2名选手为，第4组的2名选手为，第5组的1名选手为，则从这5名选手中抽取2名选手的所有情况为
，
，
，共10种，
其中第4组的2名选手中至少有1名选手人选的有
，共7种，所以第4组至少有1名选手被考官
面试的概率为.
夺冠金卷全能练考系列答案科目：高中数学 来源： 题型：
【题目】已知三棱锥的两条棱长为1，其余四条棱长为2，有下列命题：
该三棱锥的体积是
；
该三棱锥内切球的半径是
；
该三棱锥外接球的表面积是
．
其中正确的是
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，AB是半圆O的直径，C是半圆O上除A，B外的一个动点，DC垂直于半圆O所在的平面，DC∥EB，DC＝EB＝1，AB＝4.
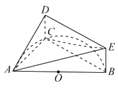
（1）证明：平面ADE⊥平面ACD；
（2）当C点为半圆的中点时，求二面角D﹣AE﹣B的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校为缓解高三学生的高考压力，经常举行一些心理素质综合能力训练活动，经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试，并将其成绩分为
、
、
、
、
五个等级，统计数据如图所示（视频率为概率），根据图中抽样调查的数据，回答下列问题：
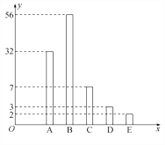
（1）试估算该校高三年级学生获得成绩为
的人数；
（2）若等级
、
、
、
、
分别对应100分、90分、80分、70分、60分，学校要求当学生获得的等级成绩的平均分大于90分时，高三学生的考前心理稳定，整体过关，请问该校高三年级目前学生的考前心理稳定情况是否整体过关？
（3）以每个学生的心理都培养成为健康状态为目标，学校决定对成绩等级为
的16名学生（其中男生4人，女生12人）进行特殊的一对一帮扶培训，从按分层抽样抽取的4人中任意抽取2名，求恰好抽到1名男生的概率..
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】四川省阆中中学某部根据运动场地的影响，但为尽大可能让学生都参与到运动会中来，在2018春季运动会中设置了五个项目，其中属于跑步类的两项，分别是200米和400米，另外三项分别为跳绳、跳远、跳高
学校要求每位学生必须参加，且只参加其中一项，学校780名同学参加各运动项目人数统计如下条形图：
其中参加跑步类的人数所占频率为
，为了了解学生身体健康与参加运动项目之间的关系，用分层抽样的方法从这780名学生中抽取13人进行分析．
1
求条形图中m和n的值以及抽取的13人中参加200米的学生人数；
2现从抽取的参加400米和跳绳两个项目中随机抽取4人，记其中参加400米跑的学生人数为X，求离散型随机变量X的分布列与数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】由单位正方形组成的无限格阵的每个单位正方形内都写有一个整数.若每个方格内的整数等于其上方和左方与其相邻的两个方格内的整数之和，且存在一行
，其中，所有方格内的数都是正整数.记下面一行为
，下面一行为
，证明：对于每个正整数
，
上不能有个方格内的整数都是0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
