
分析 设两船在B点相遇,设舰艇到达渔船的最短时间是x小时,由题设知AC=10,AB=21x,BC=9x,∠ACB=120°,由余弦定理,知(21x)2=100+(9x)2-2×10×9x×cos120°,由此能求出舰艇到达渔船的最短时间.
解答 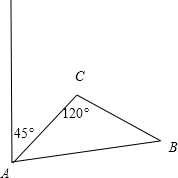 解:设两船在B点相遇,由题设作出图形,
解:设两船在B点相遇,由题设作出图形,
设舰艇到达渔船的最短时间是x小时,
则AC=10,AB=21x,BC=9x,∠ACB=120°,
由余弦定理,知(21x)2=100+(9x)2-2×10×9x×cos120°,
整理,得36x2-9x-10=0,
解得x=$\frac{2}{3}$,或x=-$\frac{5}{12}$(舍).
答:舰艇到达渔船的最短时间是$\frac{2}{3}$小时.
故答案为:$\frac{2}{3}$.
点评 本题考查解三角形在生产实际中的应用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.综合性强,是高考的重点,易错点是知识体系不牢固.解题时要注意余弦定理和数形结合思想的灵活运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
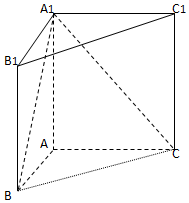 如图,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.
如图,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ③④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com