
 ,求P的坐标以及两条切线所夹劣弧长;
,求P的坐标以及两条切线所夹劣弧长;解:根据题意,设P(4,t),
(1)设两切点为C、D,则OC⊥PC,OD⊥PD,
由题意可知,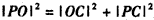 ,
,
即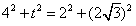 ,解得t=0,
,解得t=0,
所以点P的坐标为(4,0),
在Rt△POC中,易得∠POC=60°,所以∠DOC=120°,
所以两切线所夹劣弧长为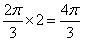 ;
;
(2)设M(x1,y1)、N(x2,y2),Q(1,0),
依题意,直线PA经过点A(-2,0),P(4,t),
可以设直线AP的方程为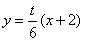 和圆联立
和圆联立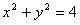 ,得到
,得到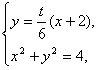 ,
,
代入消元得到,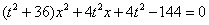 ,
,
因为直线AP经过点A(-2,0)、M(x1,y1),所以-2、x1是方程的两个根,
所以有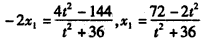 ,
,
代入直线方程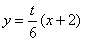 ,得
,得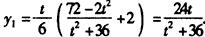 ,
,
同理,设直线BP的方程为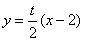 ,联立方程有
,联立方程有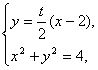 ,
,
代入消元得到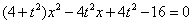 ,
,
因为直线BP经过点B(2,0)、N(x2,y2),所以2、x2是方程的两个根,
所以有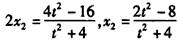 ,
,
代入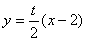 得到
得到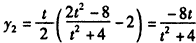 ,
,
若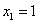 ,则
,则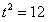 ,此时,
,此时,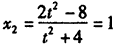 ,
,
显然M、Q、N三点在直线x=1上,即直线MN经过定点Q(1,0);
若x1≠1,则t2≠12,x2≠1,所以有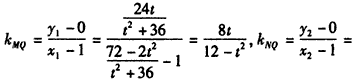
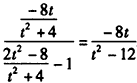 ,
,
所以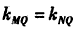 ,所以M、N、Q三点共线,
,所以M、N、Q三点共线,
即直线MN经过定点Q(1,0);
综上所述,直线MN经过定点Q(1,0)。


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
 已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为
已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知圆o:x2+y2=b2与椭圆
已知圆o:x2+y2=b2与椭圆| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com