
【题目】某地拟建一座长为640米的大桥![]() ,假设桥墩等距离分布,经设计部门测算,两端桥墩
,假设桥墩等距离分布,经设计部门测算,两端桥墩![]() 造价总共为100万元,当相邻两个桥墩的距离为
造价总共为100万元,当相邻两个桥墩的距离为![]() 米时(其中
米时(其中![]() ).中间每个桥墩的平均造价为
).中间每个桥墩的平均造价为![]() 万元,桥面每1米长的平均造价为
万元,桥面每1米长的平均造价为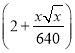 万元.
万元.

(1)试将桥的总造价表示为![]() 的函数
的函数![]() ;
;
(2)为使桥的总造价最低,试问这座大桥中间(两端桥墩![]() 除外)应建多少个桥墩?
除外)应建多少个桥墩?
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】《中国好声音(The Voice of China)》是由浙江卫视联合星空传媒旗下灿星制作强力打造的大型励志专业音乐评论节目,于2012年7月13日正式在浙江卫视播出.每期节目有四位导师参加.导师背对歌手,当每位参赛选手演唱完之前有导师为其转身,则该选手可以选择加入为其转身的导师的团队中接受指导训练.已知某期《中国好声音》中,6位选手演唱完后,四位导师为其转身的情况如下表所示:

现从这6位选手中随机抽取两人考查他们演唱完后导师的转身情况.
(1)请列出所有的基本事件;
(2)求两人中恰好其中一位为其转身的导师不少于3人,而另一人为其转身的导师不多于2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
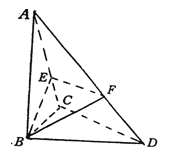
【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且![]()
(1)求证:不论![]() 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD ?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)若直角三角形两直角边长之和为12,求其周长![]() 的最小值;
的最小值;
(2)若三角形有一个内角为![]() ,周长为定值
,周长为定值![]() ,求面积
,求面积![]() 的最大值;
的最大值;
(3)为了研究边长![]() 满足
满足![]() 的三角形其面积是否存在最大值,现有解法如下:
的三角形其面积是否存在最大值,现有解法如下:![]() (其中
(其中![]() , 三角形面积的海伦公式),
, 三角形面积的海伦公式),
∴![]()
![]()
![]()
![]() ,
,
而![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
但是,其中等号成立的条件是![]() ,于是
,于是![]() 与
与![]() 矛盾,
矛盾,
所以,此三角形的面积不存在最大值.
以上解答是否正确?若不正确,请你给出正确的答案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程![]() .
.
(1)求该方程表示一条直线的条件;
(2)当![]() 为何实数时,方程表示的直线斜率不存在?求出这时的直线方程;
为何实数时,方程表示的直线斜率不存在?求出这时的直线方程;
(3)已知方程表示的直线![]() 在
在![]() 轴上的截距为-3,求实数
轴上的截距为-3,求实数![]() 的值;
的值;
(4)若方程表示的直线![]() 的倾斜角是45°,求实数
的倾斜角是45°,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图.
(1)已知![]() 、
、![]() ,
,![]() 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求![]() ,
,![]() 的值;
的值;
(2)该电子商务平台将年龄在![]() 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放80元的代金券,已经采用分层抽样的方式从参与调查的1000位上网购物者中抽取了10人,现在要在这10人中随机抽取3人进行回访,求此三人获得代金券总和
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放80元的代金券,已经采用分层抽样的方式从参与调查的1000位上网购物者中抽取了10人,现在要在这10人中随机抽取3人进行回访,求此三人获得代金券总和![]() 的分布列与数学期望.
的分布列与数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
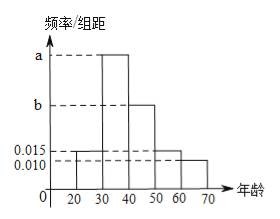
【题目】根据某电子商务平台的调查统计显示,参与调查的![]() 位上网购物者的年龄情况如右图.
位上网购物者的年龄情况如右图.
(1)已知![]() 、
、![]() 、
、![]() 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求![]() 的值;
的值;
(2)该电子商务平台将年龄在![]() 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放![]() 元的代金券,潜在消费人群每人发放
元的代金券,潜在消费人群每人发放![]() 元的代金券.已经采用分层抽样的方式从参与调查的
元的代金券.已经采用分层抽样的方式从参与调查的![]() 位上网购物者中抽取了
位上网购物者中抽取了![]() 人,现在要在这
人,现在要在这![]() 人中随机抽取
人中随机抽取![]() 人进行回访,求此三人获得代金券总和
人进行回访,求此三人获得代金券总和![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,函数
,函数![]() ,
,![]() (
(![]() 为自然对数的底数),且函数
为自然对数的底数),且函数![]() 的图象与函数
的图象与函数![]() 的图象在
的图象在![]() 处有公共的切线.
处有公共的切线.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)讨论函数![]() 的单调性;
的单调性;
(Ⅲ)证明:当![]() 时,
时,![]() 在区间
在区间![]() 内恒成立.
内恒成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com