
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:044
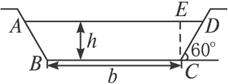
一条水渠的断面为等腰梯形(如图所示),在确定断面尺寸时,
希望在断面ABCD的面积为定值S时,使得湿周1=AB+BC+
CD最小且这样可使水流阻力小且渗透少,求此时的高h和下
底边长b。
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
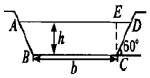
希望在断面ABCD的面积为定值S时,使得湿周1=AB+BC+
CD最小且这样可使水流阻力小且渗透少,求此时的高h和下
底边长b。
查看答案和解析>>
科目:高中数学 来源:设计选修数学-1-1苏教版 苏教版 题型:044
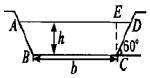
一条水渠,断面为等腰梯形,如图所示,在确定断面尺寸时,希望在断面ABCD的面积为定值S时,使得渠周长l=AB+BC+CD最小,这样可使水流阻力小,渗透少,求此时的高h和下底边长b.

查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com