
观察下列等式
12=1
12-22=-3
12-22+32=6
12-22+32-42=-10
……
照此规律,第n个等式可为________.
科目:高中数学 来源: 题型:填空题
如果正整数 的各位数字之和等于7,那么称
的各位数字之和等于7,那么称 为 “幸运数”(如:7,25,2014等均为“幸运数”), 将所有“幸运数”从小到大排成一列
为 “幸运数”(如:7,25,2014等均为“幸运数”), 将所有“幸运数”从小到大排成一列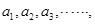 若
若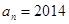 ,则
,则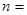 _________.
_________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
.将正奇数按下表的规律填在5列的数表中,则第20行第3列的数字与第20行第2列数字的和为________.
| | 1 | 3 | 5 | 7 |
| 15 | 13 | 11 | 9 | |
| | 17 | 19 | 21 | 23 |
| 31 | 29 | 27 | 25 | |
| … | … | … | … | … |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
设a1,a2, ,an为正整数,其中至少有五个不同值. 若对于任意的i,j(1≤i<j≤n),存在k,l(k≠l,且异于i与j)使得ai+aj=ak+al,则n的最小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
若数列 的前n项和为
的前n项和为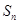 ,则下列命题:
,则下列命题:
(1)若数列 是递增数列,则数列
是递增数列,则数列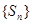 也是递增数列;
也是递增数列;
(2)数列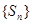 是递增数列的充要条件是数列
是递增数列的充要条件是数列 的各项均为正数;
的各项均为正数;
(3)若 是等差数列(公差
是等差数列(公差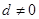 ),则
),则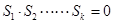 的充要条件是
的充要条件是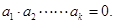
(4)若 是等比数列,则
是等比数列,则 的充要条件是
的充要条件是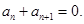
其中,正确命题的个数是( )
| A.0个 | B.1个 | C.2个 | D.3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
对于数列 ,
,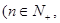
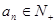 ),若
),若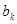 为
为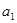 ,
,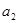 ,….,
,….,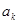 中最大值(
中最大值(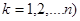 ,则称数列
,则称数列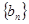 为数列
为数列 的“凸值数列”。如数列2,1,3,7,5的“凸值数列”为2,2,3,7,7;由此定义,下列说法正确的有______
的“凸值数列”。如数列2,1,3,7,5的“凸值数列”为2,2,3,7,7;由此定义,下列说法正确的有______
①递减数列 的“凸值数列”是常数列;②不存在数列
的“凸值数列”是常数列;②不存在数列 ,它的“凸值数列”还是
,它的“凸值数列”还是 本身;
本身;
③任意数列 的“凸值数列”递增数列;④“凸值数列”为1,3,3,9,的所有数列
的“凸值数列”递增数列;④“凸值数列”为1,3,3,9,的所有数列 的个数为3.
的个数为3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com