
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]()
![]() ,
,
(1)求![]()
![]()
![]() 的值,并求出
的值,并求出![]() 及数列
及数列![]() 的通项公式;
的通项公式;
(2)设![]() 求数列
求数列![]() 的前n项和
的前n项和![]()
(3)设![]()
![]() 在数列
在数列![]() 中取出
中取出![]() (
(![]() 为常数)项,按照原来的顺序排成一列,构成等比数列
为常数)项,按照原来的顺序排成一列,构成等比数列![]() .若对任意的数列
.若对任意的数列![]() ,均有
,均有![]() 试求
试求![]() 的最小值.
的最小值.
【答案】(1)![]() ;
;![]() ;
;![]() ;
;![]()
![]() ;
;![]()
![]() .(2)
.(2)![]()
 (3)最小值为
(3)最小值为![]() .
.
【解析】
(1)分别取![]() ,以及
,以及![]() 代入
代入![]() ,求出
,求出![]() ,猜想
,猜想![]() ,用数学归纳法证明即可,利用
,用数学归纳法证明即可,利用![]() ,即可求出
,即可求出![]() ;
;
(2)通过(1)裂项可知![]()
![]() ,分
,分![]() 为奇数和偶数两种情况讨论即可得出结论;
为奇数和偶数两种情况讨论即可得出结论;
(3)由(1)可知![]() ,根据条件分析子列
,根据条件分析子列![]() 的公比范围,将问题转化为求首项为1,公比为
的公比范围,将问题转化为求首项为1,公比为![]() 的等比数列的前
的等比数列的前![]() 项和.
项和.
解:(1)当![]() 时,
时,![]()
![]() ;
;
当![]() 时,
时,![]()
![]() ;
;
当![]() 时,
时,![]()
![]() ;
;
由此,猜测:![]()
![]()
下面用数学归纳法证明:
(i)当![]() 时,结论显然成立;
时,结论显然成立;
(ii)假设当![]()
![]() 时,
时,![]() ;
;
则当![]() 时,由条件,得
时,由条件,得
![]()
![]()

![]() .
.
即当![]() 时,结论也成立.
时,结论也成立.
于是,由(i),(ii)可知,对任意的![]() ,
,
均有![]() .
.
当![]() 时,
时,![]()
![]()
![]() .
.
又![]() ,
,
于是数列![]() 的通项公式为:
的通项公式为:![]()
![]() .
.
(2)因![]()
![]()
![]() .
.
当n为奇数时,
![]()
![]()
![]()
![]()
当n为偶数时,
![]()
![]()
![]()
![]()
故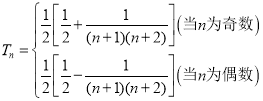

(3)因![]() ,由于数列
,由于数列![]() 的
的![]() 项子列
项子列![]() 构成等比数列,
构成等比数列,
设其公比为![]() ,则
,则
![]() .
.
因![]() ,且
,且![]()
![]()
![]() ,
,
设![]() (
(![]()
![]()
![]() ,且
,且![]() 互质)
互质)
(i)当![]() 时,因
时,因![]() ,故
,故
![]()
![]()
(ii)当![]() 时,因
时,因![]() 是数列
是数列![]() 中的项,
中的项,
故![]()
![]() .
.
从而![]()
![]()
![]()
![]()
![]()

![]()
![]()
综合(i),(ii),得:在数列![]() 中的所有
中的所有![]()
![]() 项等比子数列
项等比子数列![]() 中,
中,
其和最大的是:![]() .
.
故由题意知:![]() 的最小值为
的最小值为![]() .
.
另解(3):因![]() ,由于数列
,由于数列![]() 的
的![]()
![]() 项子列
项子列![]() 构成等比数列,
构成等比数列,
设其公比为![]() ,则
,则![]() .
.
因![]() ,且
,且![]()
![]()
![]() .
.
(i)当![]() 时,因
时,因![]() ,故
,故
![]()
![]() .
.
(ii)当![]() 时,因
时,因 ,故
,故
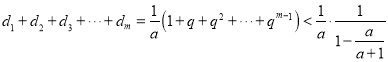
![]()
![]()
综合(i),(ii),得:在数列![]() 中的所有
中的所有![]()
![]() 项等比子数列
项等比子数列![]() 中,
中,
其和最大的是:![]() ,故由题意知:
,故由题意知:![]() 的最小值为
的最小值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】2018年辽宁省正式实施高考改革.新高考模式下,学生将根据自己的兴趣、爱好、学科特长和高校提供的“选考科目要求”进行选课.这样学生既能尊重自己爱好、特长做好生涯规划,又能发挥学科优势,进而在高考中获得更好的成绩和实现自己的理想.考改实施后,学生将在高二年级将面临着![]() 的选课模式,其中“3”是指语、数、外三科必学内容,“1”是指在物理和历史中选择一科学习,“2”是指在化学、生物、地理、政治四科中任选两科学习.某校为了更好的了解学生对“1”的选课情况,学校抽取了部分学生对选课意愿进行调查,依据调查结果制作出如下两个等高堆积条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的( )
的选课模式,其中“3”是指语、数、外三科必学内容,“1”是指在物理和历史中选择一科学习,“2”是指在化学、生物、地理、政治四科中任选两科学习.某校为了更好的了解学生对“1”的选课情况,学校抽取了部分学生对选课意愿进行调查,依据调查结果制作出如下两个等高堆积条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的( )
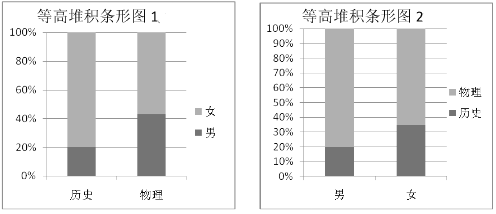
A.样本中的女生数量多于男生数量
B.样本中有学物理意愿的学生数量多于有学历史意愿的学生数量
C.样本中的男生偏爱物理
D.样本中的女生偏爱历史
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“五行”是中国古代哲学的一种系统观,广泛用于中医、堪舆、命理、相术和占卜等方面.古人把宇宙万物划分为五种性质的事物,也即分成木、火、土、金、水五大类,并称它们为“五行”.中国古代哲学家用五行理论来说明世界万物的形成及其相互关系,创造了五行相生相克理论.相生,是指两类五行属性不同的事物之间存在相互帮助,相互促进的关系,具体是:木生火,火生土,土生金,金生水,水生木.相克,是指两类五行属性不同的事物之间是相互克制的关系,具体是:木克土,土克水,水克火、火克金、金克木.现从分别标有木,火,土,金,水的![]() 根竹签中随机抽取
根竹签中随机抽取![]() 根,则所抽取的
根,则所抽取的![]() 根竹签上的五行属性相克的概率为___________.
根竹签上的五行属性相克的概率为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知圆![]() ,圆
,圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切并且与圆
外切并且与圆![]() 内切,圆心
内切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)![]() 是与圆
是与圆![]() ,圆
,圆![]() 都相切的一条直线,
都相切的一条直线,![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,当圆
两点,当圆![]() 的半径最长时,求
的半径最长时,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为整数,其前n项和为Sn.规定:若数列{an}满足前r项依次成公差为1的等差数列,从第r﹣1项起往后依次成公比为2的等比数列,则称数列{an}为“r关联数列”.
(1)若数列{an}为“6关联数列”,求数列{an}的通项公式;
(2)在(1)的条件下,求出Sn,并证明:对任意n∈N*,anSn≥a6S6;
(3)已知数列{an}为“r关联数列”,且a1=﹣10,是否存在正整数k,m(m>k),使得a1+a2+…+ak﹣1+ak=a1+a2+…+am﹣1+am?若存在,求出所有的k,m值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,其中
是直角梯形,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 上的点,且
上的点,且![]() .
.
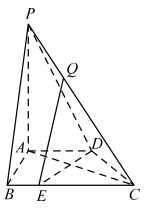
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)设![]() 为棱
为棱![]() 上的点(不与
上的点(不与![]() ,
,![]() 重合),且直线
重合),且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检测某种零件的一条生产线的生产过程,从生产线上随机抽取一批零件,根据其尺寸的数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 组,得到如图所示的频率分布直方图.若尺寸落在区间
组,得到如图所示的频率分布直方图.若尺寸落在区间![]() 之外,则认为该零件属“不合格”的零件,其中
之外,则认为该零件属“不合格”的零件,其中![]() ,
,![]() 分别为样本平均和样本标准差,计算可得
分别为样本平均和样本标准差,计算可得![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
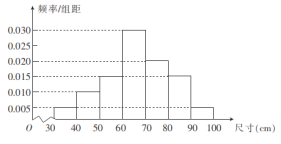
(1)若一个零件的尺寸是![]() ,试判断该零件是否属于“不合格”的零件;
,试判断该零件是否属于“不合格”的零件;
(2)工厂利用分层抽样的方法从样本的前![]() 组中抽出
组中抽出![]() 个零件,标上记号,并从这
个零件,标上记号,并从这![]() 个零件中再抽取
个零件中再抽取![]() 个,求再次抽取的
个,求再次抽取的![]() 个零件中恰有
个零件中恰有![]() 个尺寸小于
个尺寸小于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在实数集![]() 上的偶函数
上的偶函数![]() 和奇函数
和奇函数![]() 满足
满足![]() .
.
(1)求![]() 与
与![]() 的解析式;
的解析式;
(2)求证:![]() 在区间
在区间![]() 上单调递增;并求
上单调递增;并求![]() 在区间
在区间![]() 的反函数;
的反函数;
(3)设![]() (其中
(其中![]() 为常数),若
为常数),若![]() 对于
对于![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名射击运动员在进行射击训练,已知甲命中10环,9环,8环的概率分别是![]() ,
,![]() ,
,![]() ,乙命中10环,9环,8环的概率分别是
,乙命中10环,9环,8环的概率分别是![]() ,
,![]() ,
,![]() ,任意两次射击相互独立.
,任意两次射击相互独立.
(1)求甲运动员两次射击命中环数之和恰好为18的概率;
(2)现在甲、乙两人进行射击比赛,每一轮比赛两人各射击1次,环数高于对方为胜,环数低于对方为负,环数相等为平局,规定连续胜利两轮的选手为最终的胜者,比赛结束,求恰好进行3轮射击后比赛结束的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com