
【题目】在平面直角坐标系xoy中,圆的参数方程为 ![]() (φ为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为
(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为 ![]() .
.
(1)将圆的参数方程化为普通方程,在化为极坐标方程;
(2)若点P在直线l上,当点P到圆的距离最小时,求点P的极坐标.
【答案】
(1)解:将圆的参数方程,消去参数φ,
得:(x﹣2)2+ ![]() =1,
=1,
将x=ρcosθ,y=ρsinθ代入(x﹣2)2+ ![]() =1,
=1,
得圆的极坐标方程是:ρ2﹣4ρcosθ﹣4 ![]() sinθ+15=0
sinθ+15=0
(2)解:由ρcosθ=x,ρsinθ=y知,
直线l的直角坐标方程为: ![]() x+3y+4
x+3y+4 ![]() =0,其斜率是﹣
=0,其斜率是﹣ ![]() ,
,
易得直线l与圆相离,
当点P到圆的距离最小时,则点P与圆心连线与直线l垂直,即其相离是 ![]() ,
,
其方程是:y﹣2 ![]() =
= ![]() (x﹣2),即y=
(x﹣2),即y= ![]() x,
x,
联立方程组 ![]() ,解得:
,解得: ![]() ,
,
即点P的直角坐标是(﹣1,﹣ ![]() ),
),
故P的极坐标是(2, ![]() )
)
【解析】(1)求出圆的标准方程,根据x=ρcosθ,y=ρsinθ,求出极坐标方程即可;(2)求出直线l的直角坐标方程,联立方程组,求出P的坐标,从而求出P的极坐标即可.


科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点![]() 处下上至
处下上至![]() 处有两种路径.一种是从
处有两种路径.一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 沿索道乘缆车到
沿索道乘缆车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为
匀速步行,速度为![]() .在甲出发
.在甲出发![]() 后,乙从
后,乙从![]() 乘缆车到
乘缆车到![]() ,在
,在![]() 处停留
处停留![]() 后,再从
后,再从![]() 匀速步行到
匀速步行到![]() ,假设缆车匀速直线运动的速度为
,假设缆车匀速直线运动的速度为![]() ,山路
,山路![]() 长为1260
长为1260![]() ,经测量
,经测量![]() ,
,![]() .
.
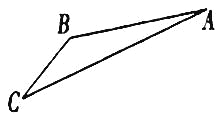
(1)求索道![]() 的长;
的长;
(2)问:乙出发多少![]() 后,乙在缆车上与甲的距离最短?
后,乙在缆车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() ,乙步行的速度应控制在什么范围内?
,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一批产品抽50件测试,其净重介于13克与19克之间,将测试结果按如下方式分成六组:第一组,净重大于等于13克且小于14克;第二组,净重大于等于14克且小于15克;…第六组,净重大于等于18克且小于19克.如图是按上述分组方法得到的频率分布直方图.设净重小于17克的产品数占抽取数的百分比为x,净重大于等于15克且小于17克的产品数为y,则从频率分布直方图中可分析出x和y分别为( )
A.0.9,35
B.0.9,45
C.0.1,35
D.0.1,45
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 满足an= ![]() +2n﹣2,n∈N* , 且S2=6.
+2n﹣2,n∈N* , 且S2=6.
(1)求数列{an}的通项公式;
(2)证明: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某社区居民购买水果和牛奶的年支出费用与购买食品的年支出费用的关系,随机调查了该社区5户家庭,得到如下统计数据表:
购买食品的年支出费用x(万元) | 2.09 | 2.15 | 2.50 | 2.84 | 2.92 |
购买水果和牛奶的年支出费用y(万元) | 1.25 | 1.30 | 1.50 | 1.70 | 1.75 |
根据上表可得回归直线方程 ![]() ,其中
,其中 ![]() ,据此估计,该社区一户购买食品的年支出费用为3.00万元的家庭购买水果和牛奶的年支出费用约为( )
,据此估计,该社区一户购买食品的年支出费用为3.00万元的家庭购买水果和牛奶的年支出费用约为( )
A.1.79万元
B.2.55万元
C.1.91万元
D.1.94万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 为定义域
为定义域![]() 上的单调函数,且存在区间
上的单调函数,且存在区间![]() (其中
(其中![]() ,使得当
,使得当![]() 时,
时,![]() 的取值范围恰为
的取值范围恰为![]() ,则称函数
,则称函数![]() 是
是![]() 上的正函数,区间
上的正函数,区间![]() 叫做函数的等域区间.
叫做函数的等域区间.
(1)已知![]() 是
是![]() 上的正函数,求
上的正函数,求![]() 的等域区间;
的等域区间;
(2)试探求是否存在![]() ,使得函数
,使得函数![]() 是
是![]() 上的正函数?若存在,请求出实数
上的正函数?若存在,请求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是数列
是数列![]() 的前n项和,
的前n项和,![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)对于正整数![]() ,已知
,已知![]() 成等差数列,求正整数
成等差数列,求正整数![]() 的值;
的值;
(3)设数列![]() 前n项和是
前n项和是![]() ,且满足:对任意的正整数n,都有等式
,且满足:对任意的正整数n,都有等式![]() 成立.求满足等式
成立.求满足等式![]() 的所有正整数n.
的所有正整数n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形![]() 的对角线
的对角线![]() 与
与![]() 相交于
相交于![]() 点,将
点,将![]() 沿对角线折起,使得平面
沿对角线折起,使得平面![]() 平面
平面![]() (如图),则下列命题中正确的是( )
(如图),则下列命题中正确的是( )
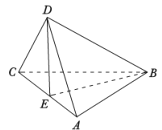
A. 直线![]() 直线
直线![]() ,且直线
,且直线![]() 直线
直线![]()
B. 直线![]() 平面
平面![]() ,且直线
,且直线![]() 平面
平面![]()
C. 平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]()
D. 平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com