
【题目】已知![]() 和
和![]() 是函数
是函数![]() 的两个零点,
的两个零点,
(1)求实数![]() 的值;
的值;
(2)设![]()
①若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
②若![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】关于![]() 的方程
的方程![]() ,给出下列四个判断:
,给出下列四个判断:
①存在实数![]() ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
②存在实数![]() ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
③存在实数![]() ,使得方程恰有6个不同的实根;
,使得方程恰有6个不同的实根;
④存在实数![]() ,使得方程恰有8个不同的实根;
,使得方程恰有8个不同的实根;
其中正确的为________(写出所有判断正确的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资人欲将5百万元奖金投入甲、乙两种理财产品,根据银行预测,甲、乙两种理财产品的收益与投入奖金![]() 的关系式分别为
的关系式分别为![]() ,其中
,其中![]() 为常数且
为常数且![]() .设对乙种产品投入奖金
.设对乙种产品投入奖金![]() 百万元,其中
百万元,其中![]() .
.
(1)当![]() 时,如何进行投资才能使得总收益
时,如何进行投资才能使得总收益![]() 最大;(总收益
最大;(总收益![]() )
)
(2)银行为了吸储,考虑到投资人的收益,无论投资人奖金如何分配,要使得总收益不低于![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln x-ax(a∈R)(e=2.718 28…是自然对数的底数).
(1)判断f(x)的单调性;
(2)当f(x)<0在(0,+∞)上恒成立时,求a的取值范围;
(3)证明:当x∈(0,+∞)时,![]() (1+x)
(1+x) ![]() <e.
<e.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=1.1x,g(x)=ln x+1,h(x)=x![]() 的图象如图所示,试分别指出各曲线对应的函数,并比较三个函数的增长差异(以1,a,b,c,d,e为分界点).
的图象如图所示,试分别指出各曲线对应的函数,并比较三个函数的增长差异(以1,a,b,c,d,e为分界点).
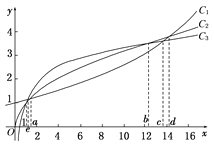
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并得到如下频率分布直方图.
,并得到如下频率分布直方图.
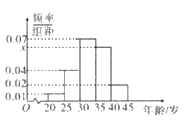
(I)求图中![]() 的值,并根据频率分布直方图统计这600名志愿者中年龄在
的值,并根据频率分布直方图统计这600名志愿者中年龄在![]() 的人数;
的人数;
(II)在抽取的100名志愿者中按年龄分层抽取5名参加区电视台“文明伴你行”节目录制,再从这5名志愿者中随机抽取2名到现场分享劝导制止行人闯红灯的经历,求至少有1名年龄不低于35岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检验某种溶剂的挥发性,在容器为1升的容器中注入溶液,然后在挥发的过程中测量剩余溶液的容积.已知溶剂注入过程中,其容积y(升)与时间t(分钟)成正比,且恰在2分钟注满;注入完成后,y与t的关系为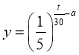 (
(![]() 为常数),如图
为常数),如图
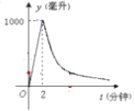
(1)求容积y与时间t之间的函数关系式.
(2)当容器中的溶液少于8毫升时,试验结束,则从注入溶液开始,至少需要经过多少分钟,才能结束试验?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂36名工人的年龄数据如下表.
工人编号 年龄 | 工人编号 年龄 | 工人编号 年龄 | 工人编号 年龄 |
1 40 | 10 36 | 19 27 | 28 34 |
2 44 | 11 31 | 20 43 | 29 39 |
3 40 | 12 38 | 21 41 | 30 43 |
4 41 | 13 39 | 22 37 | 31 38 |
5 33 | 14 43 | 23 34 | 32 42 |
6 40 | 15 45 | 24 42 | 33 53 |
7 45 | 16 39 | 25 37 | 34 37 |
8 42 | 17 38 | 26 44 | 35 49 |
9 43 | 18 36 | 27 42 | 36 39 |
(1)用系统抽样法从36名工人中抽取容量为9的样本,且在第一分段里用随机抽样法抽到的年龄数据为44,列出样本的年龄数据;
(2)计算(1)中样本的均值x和方差s2;
(3)36名工人中年龄在![]() 与
与![]() 之间有多少人?所占的百分比是多少(精确到0.01%)?
之间有多少人?所占的百分比是多少(精确到0.01%)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com