
ΓΨΧβΡΩΓΩ»γΆΦ «Έ“Ιζ2009Ρξ÷Ν2015Ρξ…ζΜνά§ΜχΈόΚΠΜ·¥ΠάμΝΩΘ®ΒΞΈΜΘΚ“ΎΕ÷Θ©ΒΡ’έœΏΆΦ.
Θ®ΔώΘ©”…’έœΏΆΦΩ¥≥ωΘ§Ω…”ΟœΏ–‘ΜΊΙιΡΘ–ΆΡβΚœy”κtΒΡΙΊœΒΘ§«κ”ΟœύΙΊœΒ ΐΦ”“‘ΥΒΟςΘΜ
Θ®ΔρΘ©Ϋ®ΝΔyΙΊ”ΎtΒΡΜΊΙιΖΫ≥ΧΘ®œΒ ΐΨΪ»ΖΒΫ0.01Θ©Θ§‘Λ≤β2017ΡξΈ“Ιζ…ζΜνά§ΜχΈόΚΠΜ·¥ΠάμΝΩΘ°
≤ΈΩΦ ΐΨίΘΚ ![]() yi=9.32Θ§
yi=9.32Θ§ ![]() tiyi=40.17Θ§
tiyi=40.17Θ§ ![]() =0.55Θ§
=0.55Θ§ ![]() Γ÷2.646Θ°
Γ÷2.646Θ°
≤ΈΩΦΙΪ ΫΘΚœύΙΊœΒ ΐr= 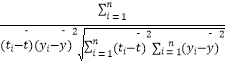 =
= 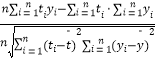
ΜΊΙιΖΫ≥Χ ![]() =
= ![]() +
+ ![]() t÷––±¬ ΚΆΫΊΨύΒΡΉν–ΓΕΰ≥ΥΙάΦΤΙΪ ΫΖ÷±πΈΣΘΚ
t÷––±¬ ΚΆΫΊΨύΒΡΉν–ΓΕΰ≥ΥΙάΦΤΙΪ ΫΖ÷±πΈΣΘΚ ![]() =
= 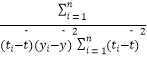 Θ§
Θ§ ![]() =
= ![]() ©¹
©¹ ![]() tΘ°
tΘ°
ΓΨ¥πΑΗΓΩΫβΘΚΘ®ΔώΘ©±δΝΩy”κtΒΡœύΙΊœΒ ΐr= ![]() Γ÷0.99Θ§ Ι Ω…”ΟœΏ–‘ΜΊΙιΡΘ–ΆΡβΚœ±δΝΩy”κtΒΡΙΊœΒΘ°
Γ÷0.99Θ§ Ι Ω…”ΟœΏ–‘ΜΊΙιΡΘ–ΆΡβΚœ±δΝΩy”κtΒΡΙΊœΒΘ°
Θ®ΔρΘ© ![]() =4Θ§
=4Θ§ ![]() =
= ![]()
![]() yi Θ§ Υυ“‘
yi Θ§ Υυ“‘ ![]() =
=  =0.1Θ§
=0.1Θ§![]() =
= ![]() ©¹
©¹ ![]() t=
t= ![]() Θ§
Θ§
Υυ“‘œΏ–‘ΜΊΙιΖΫ≥ΧΈΣ ![]() =0.1t+0.93Θ§
=0.1t+0.93Θ§
Β±t=9 ±Θ§ ![]() =0.1ΓΝ9+0.93=1.83Θ§
=0.1ΓΝ9+0.93=1.83Θ§
“ρ¥ΥΘ§Έ“Ο«Ω…“‘‘Λ≤β2017ΡξΈ“Ιζ…ζΜνά§ΜχΈόΚΠΜ·¥Πάμ1.83“ΎΕ÷
ΓΨΫβΈωΓΩΘ®ΔώΘ©«σ≥ω±δΝΩy”κtΒΡœύΙΊœΒ ΐΘ§Ω…ΒΟΫα¬έΘΜΘ®ΔρΘ©«σ≥ωΜΊΙιœΒ ΐΘ§Ω…ΒΟΜΊΙιΖΫ≥ΧΘ§Φ¥Ω…‘Λ≤β2017ΡξΈ“Ιζ…ζΜνά§ΜχΈόΚΠΜ·¥Πάμ1.83“ΎΕ÷Θ°


 –Γ―ß―ßœΑΚΟΑο ÷œΒΝ–¥πΑΗ
–Γ―ß―ßœΑΚΟΑο ÷œΒΝ–¥πΑΗ –Γ―ßΆ§≤Ϋ»ΐΝΖΚΥ–ΡΟήΨμœΒΝ–¥πΑΗ
–Γ―ßΆ§≤Ϋ»ΐΝΖΚΥ–ΡΟήΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]()
Θ®ΔώΘ©Β±![]() ±Θ§«σΚ· ΐ
±Θ§«σΚ· ΐ![]() ΒΡΒΞΒς«χΦδΘΜ
ΒΡΒΞΒς«χΦδΘΜ
Θ®ΔρΘ©Β±![]() Θ§
Θ§![]() ±Θ§÷ΛΟςΘΚ
±Θ§÷ΛΟςΘΚ![]() Θ®Τδ÷–
Θ®Τδ÷–![]() ΈΣΉ‘»ΜΕ‘ ΐΒΡΒΉ ΐΘ©.
ΈΣΉ‘»ΜΕ‘ ΐΒΡΒΉ ΐΘ©.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΓςABC÷–Θ§Ϋ«A,B,CΥυΕ‘ΒΡ±ΏΖ÷±π «a,b,c,«“![]() .
.
Θ®ΔώΘ©÷ΛΟςΘΚ![]() ΘΜ
ΘΜ
Θ®ΔρΘ©»τ![]() Θ§«σ
Θ§«σ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΚ· ΐy=logaΘ®x+2Θ©©¹1Θ®aΘΨ0Θ§aΓΌ1Θ©ΒΡΆΦœσΚψΙΐΕ®ΒψAΘ§»τΒψA‘Ύ÷±œΏmx+ny+1=0…œΘ§Τδ÷–mΘΨ0Θ§nΘΨ0Θ§‘ρ ![]() +
+ ![]() ΒΡΉν–Γ÷ΒΈΣΘ® Θ©
ΒΡΉν–Γ÷ΒΈΣΘ® Θ©
A.3+2 ![]()
B.3+2 ![]()
C.7
D.11
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΚ· ΐfΘ®xΘ©=sinΘ®ΠΊx+Π’Θ©Θ®ΠΊΘΨ0Θ§|Π’|ΘΦ ![]() Θ©ΒΡΆΦœσ»γΆΦΥυ ΨΘ§ΈΣΝΥΒΟΒΫgΘ®xΘ©=sinΠΊxΒΡΆΦœσΘ§‘ρ÷Μ“ΣΫΪfΘ®xΘ©ΒΡΆΦœσΘ® Θ©
Θ©ΒΡΆΦœσ»γΆΦΥυ ΨΘ§ΈΣΝΥΒΟΒΫgΘ®xΘ©=sinΠΊxΒΡΆΦœσΘ§‘ρ÷Μ“ΣΫΪfΘ®xΘ©ΒΡΆΦœσΘ® Θ© 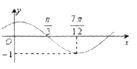
A.œρΉσΤΫ“Τ ![]() ΗωΒΞΈΜ≥ΛΕ»
ΗωΒΞΈΜ≥ΛΕ»
B.œρ”“ΤΫ“Τ ![]() ΗωΒΞΈΜ≥ΛΕ»
ΗωΒΞΈΜ≥ΛΕ»
C.œρ”“ΤΫ“Τ ![]() ΗωΒΞΈΜ≥ΛΕ»
ΗωΒΞΈΜ≥ΛΕ»
D.œρΉσΤΫ“Τ ![]() ΗωΒΞΈΜ≥ΛΕ»
ΗωΒΞΈΜ≥ΛΕ»
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏCΘΚy2=8xΒΡΫΙΒψΈΣFΘ§ΙΐFΉς«ψ–±Ϋ«ΈΣ60ΓψΒΡ÷±œΏlΘ°
Θ®1Θ©«σ÷±œΏlΒΡΖΫ≥ΧΘΜ
Θ®2Θ©«σ÷±œΏl±Μ≈ΉΈοœΏCΥυΫΊΒΟΒΡœ“≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ ΐΝ–{an} « ΉœνΈΣ’ΐ ΐΒΡΒ»≤ν ΐΝ–Θ§a1a2=3Θ§a2a3=15Θ°
Θ®1Θ©«σ ΐΝ–{an}ΒΡΆ®œνΙΪ ΫΘΜ
Θ®2Θ©…ηbn=Θ®an+1Θ©2 ![]() Θ§«σ ΐΝ–{bn}ΒΡ«ΑnœνΚΆTn Θ°
Θ§«σ ΐΝ–{bn}ΒΡ«ΑnœνΚΆTn Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ‘≤![]() ”κΉχ±ξ÷αΫΜ”Ύ
”κΉχ±ξ÷αΫΜ”Ύ![]() Θ®»γΆΦΘ©.
Θ®»γΆΦΘ©.
Θ®1Θ©Βψ![]() «‘≤
«‘≤![]() …œ≥ΐ
…œ≥ΐ![]() ΆβΒΡ»Έ“βΒψΘ®»γΆΦ1Θ©Θ§
ΆβΒΡ»Έ“βΒψΘ®»γΆΦ1Θ©Θ§![]() ”κ÷±œΏ
”κ÷±œΏ![]() ΫΜ”Ύ≤ΜΆ§ΒΡΝΫΒψ
ΫΜ”Ύ≤ΜΆ§ΒΡΝΫΒψ![]() Θ§«σ
Θ§«σ![]() ΒΡΉν–Γ÷ΒΘΜ
ΒΡΉν–Γ÷ΒΘΜ
Θ®2Θ©Βψ![]() «‘≤
«‘≤![]() …œ≥ΐ
…œ≥ΐ![]() ΆβΒΡ»Έ“βΒψΘ®»γΆΦ2Θ©Θ§÷±œΏ
ΆβΒΡ»Έ“βΒψΘ®»γΆΦ2Θ©Θ§÷±œΏ![]() ΫΜ
ΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() .…η
.…η![]() ΒΡ–±¬ ΈΣ
ΒΡ–±¬ ΈΣ![]() ΒΡ–±¬ ΈΣ
ΒΡ–±¬ ΈΣ![]() Θ§«σ÷ΛΘΚ
Θ§«σ÷ΛΘΚ ![]() ΈΣΕ®÷Β.
ΈΣΕ®÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–ΗςΕ‘Κ· ΐ÷–Θ§œύΆ§ΒΡ «Θ® Θ©
A.fΘ®xΘ©=lgx2 Θ§ gΘ®xΘ©=2lgx
B.fΘ®xΘ©=lg ![]() Θ§gΘ®xΘ©=lgΘ®x+1Θ©©¹lgΘ®x©¹1Θ©
Θ§gΘ®xΘ©=lgΘ®x+1Θ©©¹lgΘ®x©¹1Θ©
C.fΘ®uΘ©= ![]() Θ§gΘ®vΘ©=
Θ§gΘ®vΘ©= ![]()
D.fȮxȩ=xȧgȮxȩ= ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com