
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
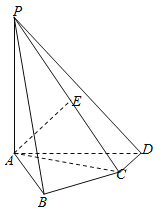
(1)求![]() 和平面
和平面![]() 所成的角的大小.
所成的角的大小.
(2)求二面角![]() 的正弦值.
的正弦值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)推导出![]() .又
.又![]() ,从而
,从而![]() 平面
平面![]() .进而
.进而![]() 为
为![]() 和平面
和平面![]() 所成的角,由此能示出
所成的角,由此能示出![]() 和平面
和平面![]() 所成的角的大小.
所成的角的大小.
(2)推导出![]() ,从而
,从而![]() 平面
平面![]() ,进而
,进而![]() 平面
平面![]() .过点
.过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,则
,则![]() 是二面角
是二面角![]() 的平面角.由此能求出二面角
的平面角.由此能求出二面角![]() 的正弦值.
的正弦值.
解:(1)在四棱锥![]() 中,∵
中,∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() .又
.又![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() .
.
故![]() 在平面
在平面![]() 内的射影为
内的射影为![]() ,从而
,从而![]() 为
为![]() 和平面
和平面![]() 所成的角.
所成的角.
在![]() 中,
中,![]() ,故
,故![]() .
.
所以![]() 和平面
和平面![]() 所成的角的大小为
所成的角的大小为![]() .
.
(2)在四棱锥![]() 中,∵
中,∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() .
.
由条件![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,∴
,∴![]() .由
.由![]() ,
,![]() ,可得
,可得![]() .
.
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() .又∵
.又∵![]() ,∴
,∴![]() 平面
平面![]() .
.
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,如图所示.
,如图所示.

∵![]() 平面
平面![]() ,
,![]() 在平面
在平面![]() 内的射影是
内的射影是![]() ,
,
∴![]() .∴
.∴![]() 是二面角
是二面角![]() 的平面角.
的平面角.
由已知∵![]() ,∴设
,∴设![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 中,
中,![]() .
.
在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,得
,得![]() .
.
在![]() 中,
中,![]() .
.
所以二面角![]() 的正弦值为
的正弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是边长为2的菱形,且
是边长为2的菱形,且![]() .四边形
.四边形![]() 是平行四边形,且
是平行四边形,且![]() .点
.点![]() ,
,![]() 在平面
在平面![]() 内的射影为
内的射影为![]() ,
,![]() ,且
,且![]() 在
在![]() 上,四棱锥
上,四棱锥![]() 的体积为2.
的体积为2.
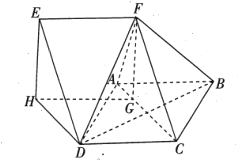
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?如果存在,是确定点
?如果存在,是确定点![]() 的位置,如果不存在,请说明理由.
的位置,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若方程![]() 所表示的曲线为
所表示的曲线为![]() ,则有以下几个命题:
,则有以下几个命题:
①当![]() 时,曲线
时,曲线![]() 表示焦点在
表示焦点在![]() 轴上的椭圆;
轴上的椭圆;
②当![]() 时,曲线
时,曲线![]() 表示双曲线;
表示双曲线;
③当![]() 时,曲线
时,曲线![]() 表示圆;
表示圆;
④存在![]() ,使得曲线
,使得曲线![]() 为等轴双曲线 .
为等轴双曲线 .
以上命题中正确的命题的序号是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信已成为人们常用的社交软件,“微信运动”是由腾讯开发的一个类似计步数据库的公众账号.手机用户可以通过关注“微信运动”公众号查看自己每天行走的步数,同时也可以和好友进行运动量的PK或点赞.现从小明的微信朋友圈内随机选取了50人(男、女各25人),并记录了他们某一天的走路步数,并将数据整理如下表:
步数 性别 | 0~3000 | 3001~6000 | 6001~9000 | 9001~12000 | >12000 |
男 | 1 | 1 | 3 | 15 | 5 |
女 | 0 | 4 | 11 | 8 | 2 |
若某人一天走路的步数超过9000步被系统评定为“积极型”,否则被系统评定为“懈怠型”。
(1)利用样本估计总体的思想,估计小明的所有微信好友中每日走路步数超过12000步的概率;
(2)根据题意完成下面的2×2列联表,并据此判断能否有99.5%的把握认为“评定类型”与“性别”有关?
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
附: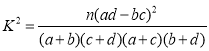 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据历史记载,美日在中途岛(Midway)海战前,美方截获了日方密码电报,据美方已破译的密码得知,日方将向某岛进行军事活动,但关键含有地点的部分却被日方换成了另一种密码.经专家研究,估计是一种密匙密码,且密匙为3位.所谓密匙密码是指:将一段英文字母的明文(未加密前原文)经过对某一组数字(即密匙)的变换,改变成了另一组英文字母成为密文(加密后的文字)例如:明文:![]() (不计空格,不计大小写)在密匙为:1 9 2的条件下,变换过程如下图所示:
(不计空格,不计大小写)在密匙为:1 9 2的条件下,变换过程如下图所示:
s | t | u | d | e | n | t |
1 | 9 | 2 | 1 | 9 | 2 | 1 |
t | c | w | e | n | p | u |
则密文为:![]() ,试根据上面信息回答下面问题:
,试根据上面信息回答下面问题:
(1)在密匙为111的条件下,填写下表,并写出密文;
s | t | u | d | e | n | t |
密文____________________.
(2)若![]()
![]() 请填写下表,并写出密匙;
请填写下表,并写出密匙;
s | t | u | d | e | n | t |
密匙为_____________.
(3)若下面即是那段包含地点(Midway)的破译不出的密文:![]() ,且此段密文也是3位密匙加密,试填写下表,写出密匙,并将此段密文翻译成明文.(不必证明,写出明文即可)
,且此段密文也是3位密匙加密,试填写下表,写出密匙,并将此段密文翻译成明文.(不必证明,写出明文即可)
c | w | b | c | f | s | o | l | l | y | d | g |
密匙为___________,明文为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①在直角梯形ABCP中,![]() ,
,![]() ,
,![]() ,
,![]() ,E,F,G分别是线段PC,PD,BC的中点,现将
,E,F,G分别是线段PC,PD,BC的中点,现将![]() 折起,使平面
折起,使平面![]() 平面ABCD如图②.
平面ABCD如图②.
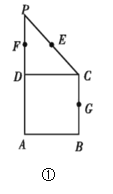
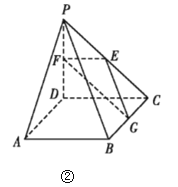
(1)求证:![]() 平面EFG;
平面EFG;
(2)求二面角G—EF—D的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com