
【题目】已知函数 ![]()
(1)求函数y=f(x)的单调递增区间;
(2)当x∈[0, ![]() ]时,函数 y=f(x)的最小值为
]时,函数 y=f(x)的最小值为 ![]() ,试确定常数a的值.
,试确定常数a的值.
【答案】
(1)
解: ![]()
= ![]() +sinx+a2sin(x+
+sinx+a2sin(x+ ![]() )
)
= ![]() sin(x+
sin(x+ ![]() )+a2sin(x+
)+a2sin(x+ ![]() )
)
=( ![]() )sin(x+
)sin(x+ ![]() ),
),
由x+ ![]() ∈[2kπ﹣
∈[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ](k∈Z)得:x∈[2kπ﹣
](k∈Z)得:x∈[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ](k∈Z),
](k∈Z),
∵ ![]() ,
,
∴ ![]() ,
,
∴函数y=f(x)的单调递增区间是:[2kπ﹣ ![]() ,2kπ﹣
,2kπ﹣ ![]() ),( 2kπ﹣
),( 2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ](k∈Z)
](k∈Z)
(2)
解:当x∈[0, ![]() ]时,x+
]时,x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],
],
∴当x+ ![]() =
= ![]() 时,函数y=f(x)取得最小值为
时,函数y=f(x)取得最小值为 ![]() ,
,
∴由已知得 ![]() =
= ![]() ,
,
∴a=±1.…
【解析】(1)利用三角函数恒等变换的应用化简函数解析式可得f(x)=( ![]() )sin(x+
)sin(x+ ![]() ),由x+
),由x+ ![]() ∈[2kπ﹣
∈[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ](k∈Z)且
](k∈Z)且 ![]() ,即可解得f(x)的单调递增区间.(2)当x∈[0,
,即可解得f(x)的单调递增区间.(2)当x∈[0, ![]() ]时,可求x+
]时,可求x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],从而可求f(x)最小值为
],从而可求f(x)最小值为 ![]() ,
,
由已知得 ![]() =
= ![]() ,即可得解.
,即可得解.


科目:高中数学 来源: 题型:
【题目】十九大提出,坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村真脱贫,坚持扶贫同扶智相结合,帮助贫困村种植蜜柚,并利用电商进行销售,为了更好地销售,现从该村的蜜柚树上随机摘下了100个蜜柚进行测重,其质量分别在![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (单位:克)中,其频率分布直方图如图所示.
(单位:克)中,其频率分布直方图如图所示.

(1)求质量落在![]() ,
, ![]() 两组内的蜜柚的抽取个数,
两组内的蜜柚的抽取个数,
(2)从质量落在![]() ,
, ![]() 内的蜜柚中随机抽取2个,求这2个蜜柚质量均小于2000克的概率;
内的蜜柚中随机抽取2个,求这2个蜜柚质量均小于2000克的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标平面中,![]() 的两个顶点为
的两个顶点为![]() ,平面内两点
,平面内两点![]() 、
、![]() 同时满足:①
同时满足:①![]() +
+![]() +
+![]() =
=![]() ;②|
;②|![]() |=|
|=|![]() |=|
|=|![]() |;③
|;③![]() ∥
∥![]() .
.
(1)求顶点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,直线
,直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 相交弦分别为
相交弦分别为![]() ,设弦
,设弦![]() 的中点分别为
的中点分别为![]() .求四边形
.求四边形![]() 的面积
的面积![]() 的最小值;
的最小值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|﹣|x|+a.
(1)若a=0,求不等式f(x)≥0的解集;
(2)若方程f(x)=x有三个不同的解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,M、N、P分别是正方体ABCD-A1B1C1D1的棱AB、BC、DD1上的点.
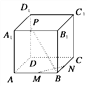
(1)若![]() ,求证:无论点P在DD1上如何移动,总有BP⊥MN;
,求证:无论点P在DD1上如何移动,总有BP⊥MN;
(2)棱DD1上是否存在这样的点P,使得平面APC1⊥平面ACC1?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:设f′(x)是函数y=f(x)的导数,f″(x)是f′(x)的导数,若方程f″(x)=0有实数解x0 , 则称点(x0 , f(x0))为函数y=f(x)的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数g(x)=2x3﹣3x2+ ![]() ,则g(
,则g( ![]() )+g(
)+g( ![]() )+…+g(
)+…+g( ![]() )=( )
)=( )
A.100
B.50
C.![]()
D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com