
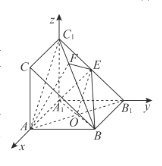
【题目】如图,直三棱柱![]() 中,侧面
中,侧面![]() 是正方形,
是正方形, ![]() 侧面
侧面![]() ,
, ![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
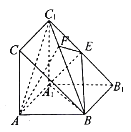
(1)求证: ![]() //平面
//平面![]() ;
;
(2)若![]() ,垂足为
,垂足为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)如图,连结![]() ,
, ![]() 交于
交于![]() ,连结
,连结![]() ,可证
,可证![]() 为
为![]() 的中位线,所以
的中位线,所以![]() ,因为
,因为![]() 面
面![]() ,
, ![]() 面
面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)由已知![]() 底面
底面![]() ,得
,得![]() 底面
底面![]() ,得
,得![]() ,
, ![]() ,又
,又![]() ,故
,故![]() ,
, ![]() ,
, ![]() 两两垂直,分别以
两两垂直,分别以![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 为原点建立空间直角坐标系,分别求出平面平面
为原点建立空间直角坐标系,分别求出平面平面![]() 的一个法向量和平面
的一个法向量和平面![]() 的一个法向量,根据二面角
的一个法向量,根据二面角![]() 的平面角为锐角,即可求得二面角
的平面角为锐角,即可求得二面角![]() 的余弦值.
的余弦值.
试题解析:
(1)如图,连结![]() ,
, ![]() 交于
交于![]() ,连结
,连结![]() ,由
,由![]() 是正方形,易得
是正方形,易得![]() 为
为![]() 的中点,从而
的中点,从而![]() 为
为![]() 的中位线,所以
的中位线,所以![]() ,因为
,因为![]() 面
面![]() ,
, ![]() 面
面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)由已知![]() 底面
底面![]() ,得
,得![]() 底面
底面![]() ,得
,得![]() ,
, ![]() ,又
,又![]() ,故
,故![]() ,
, ![]() ,
, ![]() 两两垂直,
两两垂直,
如图,分别以![]() ,
, ![]() ,
, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 为原点建立空间直角坐标系,
为原点建立空间直角坐标系,
设![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
,
设![]() ,
, ![]() ,则由
,则由![]() ,
,
得![]() ,即得
,即得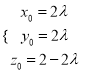 ,
,
于是![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
,
设平面![]() 的法向量是
的法向量是![]() ,则
,则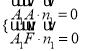 ,即
,即![]() ,
,
令![]() ,得
,得![]() .
.
又平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则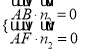 ,即
,即![]() ,
,
令![]() ,得
,得![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,则
,则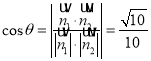 ,
,
由![]() ,面
,面![]() 面
面![]() ,可知
,可知![]() 为锐角,
为锐角,
即二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】大学生小王和小张即将参加实习,他们各从“崇尚科学,关心社会”的荆州市荆州中学、“安学、亲师、乐友、信道”的荆门市龙泉中学、“崇尚科学,追求真理”的荆门市钟祥一中、“追求卓越,崇尚一流”的襄阳市第四中学、“文明、振奋、务实、创新”的襄阳市第五中学、“千年文脉,百年一中”的宜昌市第一中学、“人走三峡,书读夷陵”的宜昌市夷陵中学这七所省重点中学中随机选择一所参加实习,两人可选同一所或者两所不同的学校,假设他们选择哪所学校是等可能的,则他们在同一个市参加实习的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且
,且![]() .
.
(1)求实数![]() 的值,并指出函数
的值,并指出函数![]() 的定义域;
的定义域;
(2)将函数![]() 图象上的所有点向右平行移动1个单位得到函数
图象上的所有点向右平行移动1个单位得到函数![]() 的图象,写出函数
的图象,写出函数![]() 的表达式;
的表达式;
(3)对于(2)中的![]() ,关于
,关于![]() 的函数
的函数![]() 在
在![]() 上的最小值为2,求
上的最小值为2,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面内,以坐标原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点![]() 、
、![]() 的极坐标分别为
的极坐标分别为![]() 、
、![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 和曲线
和曲线![]() 只有一个交点,求
只有一个交点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
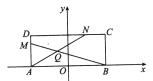
【题目】【2018衡水金卷(二)】如图,矩形![]() 中,
中, ![]() 且
且![]() ,
, ![]() 交
交![]() 于点
于点![]() .
.
(I)若点![]() 的轨迹是曲线
的轨迹是曲线![]() 的一部分,曲线
的一部分,曲线![]() 关于
关于![]() 轴、
轴、![]() 轴、原点都对称,求曲线
轴、原点都对称,求曲线![]() 的轨迹方程;
的轨迹方程;
(II)过点![]() 作曲线
作曲线![]() 的两条互相垂直的弦
的两条互相垂直的弦![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,探究
,探究![]() 是否为定值?若是,求出此定值,若不是,请说明理由.
是否为定值?若是,求出此定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,且过点
,且过点![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 为抛物线
为抛物线![]() 与椭圆
与椭圆![]() 的一个公共点,且
的一个公共点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆内一点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() 两点,设直线
两点,设直线![]() ,
,![]() (
(![]() 为坐标原点)的斜率分别为
为坐标原点)的斜率分别为![]() ,
,![]() ,若对任意
,若对任意![]() ,存在实数
,存在实数![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,O是BD的中点,CA=CB=CD=BD=2,AB=AD=![]() .
.

(1)求证:AO⊥平面BCD;
(2)求二面角O﹣AC﹣D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com