
【题目】已知点(1, ![]() )是函数f(x)=
)是函数f(x)= ![]() ax(a>0,a≠1)图象上一点,等比数列{an}的前n项和为c﹣f(n).数列{bn}(bn>0)的首项为2c,前n项和满足
ax(a>0,a≠1)图象上一点,等比数列{an}的前n项和为c﹣f(n).数列{bn}(bn>0)的首项为2c,前n项和满足 ![]() =
= ![]() +1(n≥2). (Ⅰ)求数列{an}的通项公式;
+1(n≥2). (Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{ ![]() }的前n项和为Tn , 问使Tn>
}的前n项和为Tn , 问使Tn> ![]() 的最小正整数n是多少?
的最小正整数n是多少?
【答案】(Ⅰ)解: ![]() .∴
.∴ ![]() , ∵
, ∵ ![]() ,则等比数列{an}的前n项和为c﹣
,则等比数列{an}的前n项和为c﹣ ![]()
![]() ,a2=(c﹣
,a2=(c﹣ ![]() )﹣(c﹣
)﹣(c﹣ ![]() )=
)= ![]() ,
, ![]()
由{an}为等比数列,得公比q= ![]()
∴ 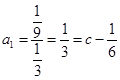 ,则c=
,则c= ![]() ,a
,a ![]()
∴ ![]()
(Ⅱ):由b1=2c=1,得s1=1
n≥2时, ![]() ,则
,则 ![]() 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.
∴ ![]() ,
, ![]() (n∈N+)
(n∈N+)
则 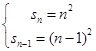 (n≥2)bn=2n﹣1,(n≥2).
(n≥2)bn=2n﹣1,(n≥2).
当n=1时,b1=1满足上式
∴ ![]()
∵ ![]() =
= ![]() =
= ![]()
∴Tn= ![]() =
= ![]() =
= ![]()
由Tn= ![]() ,得n
,得n ![]() ,则最小正整数n为59
,则最小正整数n为59
【解析】(Ⅰ)由已知求得a, ![]() ,a2=(c﹣
,a2=(c﹣ ![]() )﹣(c﹣
)﹣(c﹣ ![]() )=
)= ![]() ,
, ![]() ,得公比q=
,得公比q= ![]() ,即可写出通项;(Ⅱ)可得
,即可写出通项;(Ⅱ)可得 ![]() 是首项为1,公差为1的等差数列.由
是首项为1,公差为1的等差数列.由 ![]() (n≥2)bn=2n﹣1,(n≥2).
(n≥2)bn=2n﹣1,(n≥2). ![]() =
= ![]() =
= ![]() ,累加求得Tn=
,累加求得Tn= ![]() ,得n
,得n ![]() ,即可得最小正整数n.
,即可得最小正整数n.


科目:高中数学 来源: 题型:
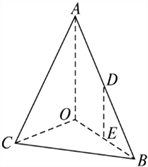
【题目】如图,在三棱锥![]() 中,
中, ![]() ⊥平面
⊥平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 的中点.(19)
的中点.(19)
(I)求![]() 到平面
到平面![]() 的距离;
的距离;
(II)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() ∥平面
∥平面![]() ,若存在,试确定
,若存在,试确定![]() 的位置,并证明此点满足要求;若不存在,请说明理由.
的位置,并证明此点满足要求;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是等比数列,且b2=3,b3=9,a1=b1 , a14=b4 . (Ⅰ)求{an}的通项公式;
(Ⅱ)设cn=an+bn , 求数列{cn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足f(x+1)= ![]() ,且f(x)在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
,且f(x)在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
A.f(sinα)>f(sinβ)
B.f(cosα)>f(cosβ)
C.f(sinα)>f(cosβ)
D.f(sinα)<f(cosβ)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.
,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N. 
(1)求椭圆C的方程;
(2)求 ![]()
![]() 的最小值;
的最小值;
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:|OR||OS|是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察以下三个等式: sin215°﹣sin245°+sin15°cos45°=﹣ ![]() ,
,
sin220°﹣sin250°+sin20°cos50°=﹣ ![]() ,
,
sin230°﹣sin260°+sin30°cos60°=﹣ ![]() ;
;
猜想出一个反映一般规律的等式: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com