
【题目】已知函数![]() .
.
(1)若曲线![]() 过点
过点![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(3)若函数![]() 有两个不同的零点
有两个不同的零点![]() ,
, ![]() ,求证:
,求证: ![]() .
.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:(1)因为点![]() 在曲线
在曲线![]() 上,所以
上,所以![]() ,解得
,解得![]() ,利用导数求得斜率为
,利用导数求得斜率为![]() ,故切线为
,故切线为![]() ;(2)
;(2)![]() ,将
,将![]() 分成
分成![]() 四类,讨论函数的单调区间进而求得最大值;(3)不妨设
四类,讨论函数的单调区间进而求得最大值;(3)不妨设![]() ,因为
,因为![]() ,所以
,所以![]() ,
,![]() ,要证明
,要证明![]() ,即证明
,即证明![]() ,令
,令![]() ,即证
,即证![]() ,令
,令![]() (
(![]() ),利用导数求得
),利用导数求得![]() 的最小值大于零即可.
的最小值大于零即可.
试题解析:
(1)因为点![]() 在曲线
在曲线![]() 上,所以
上,所以![]() ,解得
,解得![]() .
.
因为![]() ,所以切线的斜率为0,
,所以切线的斜率为0,
所以切线方程为![]() .
.
(2)因为![]() ,
,
①当![]() 时,
时, ![]() ,
, ![]() ,
,
所以函数![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ;
;
②当![]() ,即
,即![]() 时,
时, ![]() ,
, ![]() ,
,
所以函数![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ;
;
③当![]() ,即
,即![]() 时,
时,
函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
则![]() ;
;
④当![]() ,即
,即![]() 时,
时, ![]() ,
, ![]() ,
,
函数![]() 在
在![]() 上单调递减,则
上单调递减,则![]() .
.
综上,当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() .
.
(3)不妨设![]() ,
,
因为![]() ,
,
所以![]() ,
,![]() ,
,
可得![]() ,
, ![]() ,
,
要证明![]() ,即证明
,即证明![]() ,也就是
,也就是![]() ,
,
因为![]() ,
,
所以即证明![]() ,
,
即![]() ,
,
令![]() ,则
,则![]() ,于是
,于是![]() ,
,
令![]() (
(![]() ),
),
则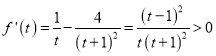 ,
,
故函数![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() ,即
,即![]() 成立,所以原不等式成立.
成立,所以原不等式成立.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() 是椭圆的焦点,直线
是椭圆的焦点,直线![]() 的斜率为
的斜率为![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,当
两点,当![]() 的面积最大时,求直线
的面积最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).
).
(1)若曲线![]() 在点
在点![]() 处的切线经过点
处的切线经过点![]() ,求
,求![]() 的值;
的值;
(2)若![]() 在区间
在区间![]() 上存在极值点,判断该极值点是极大值点还是极小值点,并求
上存在极值点,判断该极值点是极大值点还是极小值点,并求![]() 的取值范围;
的取值范围;
(3)若当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某物体一天中的温度![]() 是时间
是时间![]() 的函数,已知
的函数,已知![]() ,其中温度的单位是
,其中温度的单位是![]() ,时间的单位是小时,规定中午12:00相应的
,时间的单位是小时,规定中午12:00相应的![]() ,中午12:00以后相应的
,中午12:00以后相应的![]() 取正数,中午12:00以前相应的
取正数,中午12:00以前相应的![]() 取负数(例如早上8:00相应的
取负数(例如早上8:00相应的![]() ,下午16:00相应的
,下午16:00相应的![]() ),若测得该物体在中午12:00的温度为
),若测得该物体在中午12:00的温度为![]() ,在下午13:00的温度为
,在下午13:00的温度为![]() ,且已知该物体的温度在早上8:00与下午16:00有相同的变化率.
,且已知该物体的温度在早上8:00与下午16:00有相同的变化率.
(1)求该物体的温度![]() 关于时间
关于时间![]() 的函数关系式;
的函数关系式;
(2)该物体在上午10:00至下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某物体一天中的温度![]() 是时间
是时间![]() 的函数,已知
的函数,已知![]() ,其中温度的单位是
,其中温度的单位是![]() ,时间的单位是小时,规定中午12:00相应的
,时间的单位是小时,规定中午12:00相应的![]() ,中午12:00以后相应的
,中午12:00以后相应的![]() 取正数,中午12:00以前相应的
取正数,中午12:00以前相应的![]() 取负数(例如早上8:00相应的
取负数(例如早上8:00相应的![]() ,下午16:00相应的
,下午16:00相应的![]() ),若测得该物体在中午12:00的温度为
),若测得该物体在中午12:00的温度为![]() ,在下午13:00的温度为
,在下午13:00的温度为![]() ,且已知该物体的温度在早上8:00与下午16:00有相同的变化率.
,且已知该物体的温度在早上8:00与下午16:00有相同的变化率.
(1)求该物体的温度![]() 关于时间
关于时间![]() 的函数关系式;
的函数关系式;
(2)该物体在上午10:00至下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间![]() 内的频率之比为
内的频率之比为![]() .
.
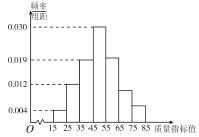
(1)求这些产品质量指标值落在区间![]() 内的频率;
内的频率;
(2)若将频率视为概率,从该企业生产的这种产品中随机抽取3件,记这3件产品中质量指标值位于区间![]() 内的产品件数为
内的产品件数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了降低能源消耗,某冷库内部要建造可供使用20年的隔热层,每厘米厚的隔热层建造成本为4万元,又知该冷库每年的能源消耗费用![]() (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度![]() (单位:
(单位: ![]() )满足关系
)满足关系![]() ,若不建隔热层,每年能源消耗为8万元.设
,若不建隔热层,每年能源消耗为8万元.设![]() 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用![]() 达到最小?并求最小值.
达到最小?并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如下柱状图:

(1)从样本中任意选取2名学生,求恰好有一名学生的打分不低于4分的概率;
(2)若以这100人打分的频率作为概率,在该校随机选取2名学生进行打分(学生打分之间相互独立)记![]() 表示两人打分之和,求
表示两人打分之和,求![]() 的分布列和
的分布列和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列程序运行后,a,b,c的值各等于什么?

(1)_____________________________________________________________.
(2)_____________________________________________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com