Question

【题目】已知数列的首项为1，且，数列满足，，对任意，都有.

（1）求数列、的通项公式；

（2）令，数列的前项和为.若对任意的，不等式恒成立，试求实数的取值范围.

Answer 1

【答案】（Ⅰ）， ；（Ⅱ）

【解析】

试题（1）由，得，又，两式相减得，整理得，即，又因为，，

利用累积法得，

从而可求出数学的通项公式为；

在数列中，由，得，且，

所以数学是以首项为，公比为的等比数列，从而数列的通项公式为.

（2）由题意得，

，

两式相减得，

由等比数列前项和公式可求得，

由不等式恒成立，得恒成立，

即（）恒成立，

构造函数（），

当时，恒成立，则不满足条件；

当时，由二次函数性质知不恒成立；

当时，恒成立，则满足条件．

综上所述，实数的取值范围是．

试题解析：（1）∵，∴()，两式相减得，，

∴，即()，又因为，，从而

∴()，

故数列的通项公式()．

在数列中，由，知数列是等比数列，首项、公比均为，

∴数列的通项公式．

（2）∴①

∴②

由①-②，得，

∴，

不等式即为，

即（）恒成立．

方法一、设（），

当时，恒成立，则不满足条件；

当时，由二次函数性质知不恒成立；

当时，恒成立，则满足条件．

综上所述，实数λ的取值范围是．

方法二、也即（）恒成立，

令．则，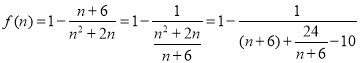

由，单调递增且大于0，∴单调递增∴

∴实数λ的取值范围是．