
【题目】在△ABC中,AC=6,cos B=![]() ,C=
,C=![]() .
.
(1)求AB的长;
(2)求cos![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由同角函数基本关系式得sin B=![]() ,求出sin B=
,求出sin B=![]() ;再由正弦定理
;再由正弦定理![]() 求出
求出![]() . (2)由三角形三个内角和的关系得出A=π-(B+C);再利用诱导公式求出cos A=-cos Bcos
. (2)由三角形三个内角和的关系得出A=π-(B+C);再利用诱导公式求出cos A=-cos Bcos![]() +sin Bsin
+sin Bsin![]() =-
=-![]() ;接着求出sin A==
;接着求出sin A==![]() ;最后利用诱导公式求出cos
;最后利用诱导公式求出cos![]() =cos Acos
=cos Acos![]() +sin A·sin
+sin A·sin![]() =
=![]() .
.
试题解析:
(1)因为cos B=![]() ,0<B<π,
,0<B<π,
所以sin B=![]() =
=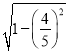 =
=![]() ,
,
由正弦定理知, ![]() ,
,
所以 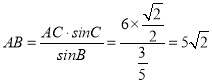 .
.
(2)在三角形ABC中A+B+C=π,
所以A=π-(B+C).
于是cos A=-cos(B+C)
=-cos![]()
=-cos Bcos![]() +sin Bsin
+sin Bsin![]() ,
,
又cos B=![]() ,sin B=
,sin B=![]() ,
,
故cos A=-![]() ×
×![]() +
+![]() ×
×![]() =-
=-![]() ,
,
因为0<A<π,所以sin A=![]() =
=![]() .
.
因此cos![]() =cos Acos
=cos Acos![]() +sin A·sin
+sin A·sin![]() =-
=-![]() ×
×![]() +
+![]() ×
×![]() =
=![]() .
.
【点晴】
解三角形的常用的与三内角及三边有关的知识有:同角函数基本关系式、三个内角关系、正弦定理、余弦定理及其推论、三角形的面积公式等,这些公式一定要熟记才能做到灵活应用.


科目:高中数学 来源: 题型:
【题目】若![]() ,
, ![]() ,则实数
,则实数![]() 的取值范围为__________.
的取值范围为__________.
【答案】![]()
【解析】当m=0时,符合题意。
当m≠0时, ![]() ,则0<m<4,
,则0<m<4,
则0m<4
答案为: ![]() .
.
点睛:解本题的关键是处理二次函数在区间上大于0的恒成立问题,对于二次函数的研究一般从以几个方面研究:
一是,开口;
二是,对称轴,主要讨论对称轴与区间的位置关系;
三是,判别式,决定于x轴的交点个数;
四是,区间端点值.
【题型】填空题
【结束】
15
【题目】已知椭圆![]() :
: ![]() 的右焦点为
的右焦点为![]() ,
, ![]() 为直线
为直线![]() 上一点,线段
上一点,线段![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;
(3)在区间[-1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,则( )
A.△A1B1C1和△A2B2C2都是锐角三角形
B.△A1B1C1和△A2B2C2都是钝角三角形
C.△A1B1C1是钝角三角形,△A2B2C2是锐角三角形
D.△A1B1C1是锐角三角形,△A2B2C2是钝角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知矩形![]() 的长为
的长为![]() ,宽为
,宽为![]() ,
, ![]() 、
、![]() 边分别在
边分别在![]() 轴、
轴、![]() 轴的正半轴上,
轴的正半轴上, ![]() 点与坐标原点重合.将矩形折叠,是
点与坐标原点重合.将矩形折叠,是![]() 点落在线段
点落在线段![]() 上.
上.
(Ⅰ)当![]() 点落在
点落在![]() 中点时,求折痕所在的直线方程.
中点时,求折痕所在的直线方程.
(Ⅱ)若折痕所在直线的斜率为![]() ,求折痕所在的直线方程与
,求折痕所在的直线方程与![]() 轴的交点坐标.(答案中可以出现
轴的交点坐标.(答案中可以出现![]() )
)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在每年的3月份,濮阳市政府都会发动市民参与到植树绿化活动中去林业管理部门为了保证树苗的质量都会在植树前对树苗进行检测,现从甲、乙两种树苗中各抽测了![]() 株树苗,量出它们的高度如下(单位:厘米),
株树苗,量出它们的高度如下(单位:厘米),
甲:37,21,31,20,29,19,32,23,25,33;
乙:10,30,47,27,46,14,26,10,44,46.
(1)画出两组数据的茎叶图并根据茎叶图对甲、乙两种树苗的高度作比较,写出两个统计结论;
(2)设抽测的![]() 株甲种树苗高度平均值为
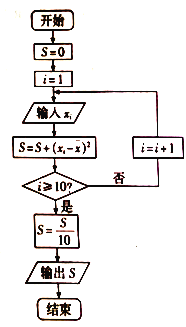
株甲种树苗高度平均值为![]() ,将这
,将这![]() 株树苗的高度依次输人,按程序框(如图)进行运算,问输出的
株树苗的高度依次输人,按程序框(如图)进行运算,问输出的![]() 大小为多少?并说明
大小为多少?并说明![]() 的统计学意义,
的统计学意义,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,随机抽取了![]() 个试销售数据,得到第
个试销售数据,得到第![]() 个销售单价
个销售单价![]() (单位:元)与销售
(单位:元)与销售![]() (单位:件)的数据资料,算得
(单位:件)的数据资料,算得
![]()
(1)求回归直线方程![]() ;
;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是![]() 元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润-销售收入-成本)
元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润-销售收入-成本)
附:回归直线方程![]() 中,
中, ,其中
,其中![]() 是样本平均值.
是样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线![]() 的焦点
的焦点![]() ,斜率为
,斜率为![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,且
两点,且![]() .
.
(1)求该抛物线![]() 的方程;
的方程;
(2)已知抛物线上一点![]() ,过点
,过点![]() 作抛物线的两条弦
作抛物线的两条弦![]() 和
和![]() ,且
,且![]() ,判断直线
,判断直线![]() 是否过定点?并说明理由.
是否过定点?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com