
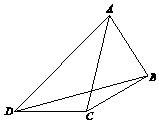
 在如图所示的平面图形中,已知CD=$\sqrt{2}$,∠BCA=45°,∠ACD=105°,∠CDB=15°,∠BDA=30°.
在如图所示的平面图形中,已知CD=$\sqrt{2}$,∠BCA=45°,∠ACD=105°,∠CDB=15°,∠BDA=30°.分析 (Ⅰ)推导出∠BCD=150°,∠DBC=15°,从而BC=DC=$\sqrt{2}$,△BCD的面积${S}_{△BCD}=\frac{1}{2}×BC×DC×sin∠BCD$,由此能求出结果.
(Ⅱ)先求出∠DAC=30°,∠ADC=45°,由此利用正弦定理能求出AC,利用余弦定理能求出出AB.
解答 解:(Ⅰ)∵CD=$\sqrt{2}$,∠BCA=45°,∠ACD=105°,∠CDB=15°,∠BDA=30°.
∴∠BCD=105°+45°=150°,∠DBC=15°,
∴BC=DC=$\sqrt{2}$,
∴△BCD的面积${S}_{△BCD}=\frac{1}{2}×BC×DC×sin∠BCD$=$\frac{1}{2}×\sqrt{2}×\sqrt{2}×sin120°$=$\frac{\sqrt{3}}{2}$.
(Ⅱ)∠DAC=180°-(15°+30°)-105°=30°,∠ADC=30°+15°=45°,
由正弦定理得:$\frac{DC}{sin∠DAC}=\frac{AC}{sin∠ADC}$,
∴AC=$\frac{DC×sin∠ADC}{sin∠DAC}$=$\frac{\sqrt{2}×sin45°}{sin30°}$=2.
由余弦定理得:
AB=$\sqrt{A{C}^{2}+{BC}^{2}-2×AC×BC×cos∠ACB}$=$\sqrt{4+2-2×2×\sqrt{2}×cos45°}$=$\sqrt{2}$.
点评 本题考查三角形面积的求法,考查三角形边长的求法,考查正弦定理、余弦定理等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{4}$,+∞) | B. | (2,+∞) | C. | (-∞,2) | D. | (-1,$\frac{1}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9π}{2}$ | B. | $\frac{125π}{6}$ | C. | $\frac{32π}{3}$ | D. | 36π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 | 患流感 | 未患流感 |
| 服用药 | 2 | 18 |
| 未服用药 | 8 | 12 |
| P(K2>k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 0.05 | B. | 0.025 | C. | 0.01 | D. | 0.005 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |m|>|n| | B. | ($\frac{1}{2}$)m<($\frac{1}{2}$)n | C. | sinm>sinn | D. | m${\;}^{\frac{1}{2}}$>n${\;}^{\frac{1}{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com