
【题目】已知数列{an}中,a1=1,a2=a,且an+1=k(an+an+2)对任意正整数n都成立,数列{an}的前n项和为Sn.
(1)若![]() ,且S2019=2019,求a;
,且S2019=2019,求a;
(2)是否存在实数k,使数列{an}是公比不为1的等比数列,且任意相邻三项am,am+1,am+2按某顺序排列后成等差数列,若存在,求出所有k的值;若不存在,请说明理由;
(3)若![]() ,求Sn.
,求Sn.
【答案】(1) a=1;(2)存在满足要求的实数k有且仅有一个![]()
![]() ;(3) Sn=
;(3) Sn=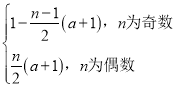
【解析】
(1)由题意求得首项为1,公差d=a-1,结合等差数列前n项和公式列方程可得a;
(2)假设存在满足题意的实数k,分类讨论可得k;
(3)k=![]()
![]() ,an+1=
,an+1=![]()
![]() (an+an+2),an+2+an+1=
(an+an+2),an+2+an+1=![]() (an+1+an),an+3+an+2=
(an+1+an),an+3+an+2=![]() (an+2+an+1)=an+1+an,结合题意分类讨论,然后分组求和可得Sn.
(an+2+an+1)=an+1+an,结合题意分类讨论,然后分组求和可得Sn.
解:(1)k=![]() ,an+1=
,an+1=![]() (an+an+2),
(an+an+2),
∴数列{an}为等差数列,
∵a1=1,a2=a,∴公差d=a-1,
∴S2019=2019=2019+![]() ×(a-1),解得a=1;
×(a-1),解得a=1;
(2)设数列{an}是公比不为1的等比数列,则它的公比q=![]() =a,
=a,
∴am=am-1,am+1=am,am+2=am+1,任意相邻三项
am,am+1,am+2按某顺序排列后成等差数列,
①an+1为等差中项,则2am+1=am+am+2.
即am-1+am+1=2am,解得a=1,不合题意;
②am为等差中项,则2am=am+1+am+2,
即2am-1=am+1+am,化简a2+a-2=0,解得a=-2或a=1(舍去);
③若am+2为等差中项,则2am+2=am+1+am,
即2am+1=am+am-1,化简得:2a2-a-1=0,解得a=![]()
![]() ;
;
∴k=![]() =
=![]() =
=![]() =
=![]()
![]() .
.
综上可得,满足要求的实数k有且仅有一个![]()
![]() ;
;
(3)k=![]()
![]() ,则an+1=
,则an+1=![]()
![]() (an+an+2),
(an+an+2),
∴an+2+an+1=![]() (an+1+an),an+3+an+2=
(an+1+an),an+3+an+2=![]() (an+2+an+1)=an+1+an,
(an+2+an+1)=an+1+an,
当n是偶数时,Sn=a1+a2+…+an=(a1+a2)+…+(an-1+an)
=![]() (a1+a2)=
(a1+a2)=![]() (a+1).
(a+1).
当n是奇数时,Sn=a1+(a2+a3)+…+(an-1+an)
=1+![]() (a2+a3)=1+
(a2+a3)=1+![]() [-(a1+a2)]=1
[-(a1+a2)]=1![]()
![]() (a+1)(n≥1),
(a+1)(n≥1),
n=1也适合上式,
综上可得,Sn=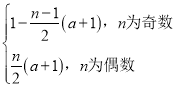 .
.


科目:高中数学 来源: 题型:
【题目】杨辉三角,是二项式系数在三角形中的一种几何排列.在欧洲,这个表叫做帕斯卡三角形,帕斯卡(1623-1662)是在1654年发现这一规律的.我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,这是我国数学史上的一个伟大成就.如图所示,在“杨辉三角”中,去除所有为1的项,依次构成数列![]() ,则此数列前135项的和为( )
,则此数列前135项的和为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,过点
,过点![]() 向圆
向圆![]() 引两条切线
引两条切线![]() ,
,![]() ,切点为
,切点为![]() ,
,![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,则直线
,则直线![]() 的方程为____________;若
的方程为____________;若![]() 为直线
为直线![]() 上一动点,则直线
上一动点,则直线![]() 经过定点__________.
经过定点__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着电子阅读的普及,传统纸质媒体遭受到了强烈的冲击.某杂志社近9年来的纸质广告收入如下表所示:

根据这9年的数据,对![]() 和
和![]() 作线性相关性检验,求得样本相关系数的绝对值为0.243;
作线性相关性检验,求得样本相关系数的绝对值为0.243;
根据后5年的数据,对![]() 和
和![]() 作线性相关性检验,求得样本相关系数的绝对值为0.984.
作线性相关性检验,求得样本相关系数的绝对值为0.984.
(1)如果要用线性回归方程预测该杂志社2019年的纸质广告收入,现在有两个方案,
方案一:选取这9年数据进行预测,方案二:选取后5年数据进行预测.
从实际生活背景以及线性相关性检验的角度分析,你觉得哪个方案更合适?
附:相关性检验的临界值表:
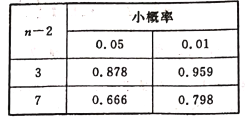
(2)某购物网站同时销售某本畅销书籍的纸质版本和电子书,据统计,在该网站购买该书籍的大量读者中,只购买电子书的读者比例为![]() ,纸质版本和电子书同时购买的读者比例为
,纸质版本和电子书同时购买的读者比例为![]() ,现用此统计结果作为概率,若从上述读者中随机调查了3位,求购买电子书人数多于只购买纸质版本人数的概率.
,现用此统计结果作为概率,若从上述读者中随机调查了3位,求购买电子书人数多于只购买纸质版本人数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面命题正确的是( )
A.“![]() ”是“
”是“![]() ”的 充 分不 必 要条件
”的 充 分不 必 要条件
B.命题“若![]() ,则
,则![]() ”的 否 定 是“ 存 在
”的 否 定 是“ 存 在![]() ,则
,则![]() ”.
”.
C.设![]() ,则“
,则“![]() 且
且![]() ”是“
”是“![]() ”的必要而不充分条件
”的必要而不充分条件
D.设![]() ,则“
,则“![]() ”是“
”是“![]() ”的必要 不 充 分 条件
”的必要 不 充 分 条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,过
,过![]() 的直线
的直线![]() 与
与![]() 轴交于
轴交于![]() 点,与
点,与![]() 轴交于
轴交于![]() 点,记
点,记![]() 与坐标轴围成的三角形
与坐标轴围成的三角形![]() 的面积为
的面积为![]() .
.
(1)若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若![]() 、
、![]() 都在正半轴上,求
都在正半轴上,求![]() 的最小值;
的最小值;
(3)写出面积![]() 的取值范围与直线
的取值范围与直线![]() 条数的对应关系.(不需要证明)
条数的对应关系.(不需要证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的长轴长为4,焦距为
的长轴长为4,焦距为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
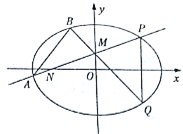
(Ⅱ)过动点![]() 的直线交
的直线交![]() 轴与点
轴与点![]() ,交
,交![]() 于点
于点![]() (
(![]() 在第一象限),且
在第一象限),且![]() 是线段
是线段![]() 的中点.过点
的中点.过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于另一点
于另一点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.
(ⅰ)设直线![]() 的斜率分别为
的斜率分别为![]() ,证明
,证明![]() 为定值;
为定值;
(ⅱ)求直线![]() 的斜率的最小值.
的斜率的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com