Question

（本题满分14分）

给定椭圆，称圆心在原点，半径为的圆是椭圆Ｃ的“准圆”.若椭圆C的一个焦点为，其短轴上的一个端点到Ｆ的距离为．

（Ⅰ）求椭圆Ｃ的方程和其“准圆”方程；

（Ⅱ）点P是椭圆C的“准圆”上的一个动点，过点P作直线，使得与椭圆C都只有一个交点，且分别交其“准圆”于点M，N ．

（1）当P为“准圆”与轴正半轴的交点时，求的方程；

（2）求证：|MN|为定值．

 

 

 

Answer 1

（本题满分14分）

解：（I）因为，所以

所以椭圆的方程为，    …………………………………3分

又=2, 所以准圆的方程为_. ………………………4分

（II）（1）因为准圆与轴正半轴的交点为P（0，2）,

设过点P（0，2），且与椭圆有一个公共点的直线为, 

所以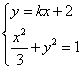，消去y ，得到 , …………6分

因为椭圆与只有一个公共点, 所以 , 

解得.所以方程为.          ……………9分

（2）①当中有一条无斜率时，不妨设无斜率，

因为与椭圆只有一个公共点，则其方程为或，

当方程为时，此时与准圆交于点，

此时经过点(或)且与椭圆只有一个公共点的直线是

(或)，即为(或)，显然直线垂直；

同理可证 方程为时，直线垂直.        ……………11分

② 当都有斜率时，设点，其中，

设经过点与椭圆只有一个公共点的直线为,

则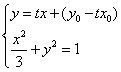，消去得到，

即,

，

经过化简得到:,

因为，所以有,

设的斜率分别为,因为与椭圆都只有一个公共点，

所以满足上述方程,

所以，即垂直.       ………………………………………13分

综合①②知：

因为经过点，又分别交其准圆于点M，N，且垂直，

所以线段MN为准圆的直径，所以|ＭＮ|＝４. ……………14分