练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    将n个正数1，2，3，…，填入n×n方格中，使得每行、每列、每条对角线上的数字的和相等，这个方形就叫做n阶幻方，记f(n)为n阶幻方对角线上数字之和，如：下图就是一个3阶幻方，可知f(3)=15，那么f(4)等于（    ）

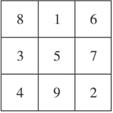
    A.32           B.33               C.34                D.35

    C

    解析:∵1+2+3+…+16==136,?

    ∴f(4)==34.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知两个正数a，b，可按规则c=ab+a+b扩充为一个新数c，在a，b，c三个数中取两个较大的数，按上述规则扩充得到一个新数，依次下去，将每扩充一次得到一个新数称为一次操作．
    （1）若a=1，b=3，按上述规则操作三次，扩充所得的数是
    255
    255
    ；
    （2）若p＞q＞0，经过6次操作后扩充所得的数为（q+1）m（p+1）n-1（m，n为正整数），则m，n的值分别为
    8，13
    8，13
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给定有限个正数满足条件T:每个数都不大于50且总和L=1 275.现将这些数按下列要求进行分组,每组数之和不大于150且分组的步骤是:?

    首先,从这些数中选择这样一些数构成第一组,使得150与这组数之和的差r1与所有可能的其他选择相比是最小的,r1称为第一组余差；?

    然后,在去掉已选入第一组的数后,对余下的数按第一组的选择方式构成第二组,这时的余差为r2；如此继续构成第三组(余差为r3)、第四组(余差为r4)、…,直至第N组(余差为rn)把这些数全部分完为止.?

    (1)判断r1,r2,…,rn的大小关系,并指出除第N组外的每组至少含有几个数；?

    (2)当构成第n(n＜N)组后,指出余下的每个数与rn的大小关系,并证明

    (3)对任何满足条件T的有限个正数,证明N≤11.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知两个正数a，b，可按规则c=ab+a+b扩充为一个新数c，在a，b，c三个数中取两个较大的数，按上述规则扩充得到一个新数，依次下去，将每扩充一次得到一个新数称为一次操作．
    （1）若a=1，b=3，按上述规则操作三次，扩充所得的数是________；
    （2）若p＞q＞0，经过6次操作后扩充所得的数为（q+1）m（p+1）n-1（m，n为正整数），则m，n的值分别为________．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年北京市朝阳区高三（上）期末数学试卷（理科）（解析版） 题型：填空题

    已知两个正数a，b，可按规则c=ab+a+b扩充为一个新数c，在a，b，c三个数中取两个较大的数，按上述规则扩充得到一个新数，依次下去，将每扩充一次得到一个新数称为一次操作．
    （1）若a=1，b=3，按上述规则操作三次，扩充所得的数是    ；
    （2）若p＞q＞0，经过6次操作后扩充所得的数为（q+1）m（p+1）n-1（m，n为正整数），则m，n的值分别为    ．

    查看答案和解析>>

    同步练习册答案