
【题目】某地自来水苯超标,当地自来水公司对水质检测后,决定在水中投放一种药剂来净化水质,已知每投放质量为![]() 的药剂后,经过
的药剂后,经过![]() 天该药剂在水中释放的浓度
天该药剂在水中释放的浓度![]() (毫克/升)满足
(毫克/升)满足![]() ,其中
,其中 ,当药剂在水中的浓度不低于5(毫克/升)时称为有效净化;当药剂在水中的浓度不低于5(毫克/升)且不高于10(毫克/升)时称为最佳净化.
,当药剂在水中的浓度不低于5(毫克/升)时称为有效净化;当药剂在水中的浓度不低于5(毫克/升)且不高于10(毫克/升)时称为最佳净化.
(Ⅰ)如果投放的药剂质量为![]() ,试问自来水达到有效净化一共可持续几天?
,试问自来水达到有效净化一共可持续几天?
(Ⅱ)如果投放的药剂质量为![]() ,为了使在9天(从投放药剂算起包括9天)之内的自来水达到最佳净化,试确定应该投放的药剂质量
,为了使在9天(从投放药剂算起包括9天)之内的自来水达到最佳净化,试确定应该投放的药剂质量![]() 的最小值.
的最小值.
【答案】(Ⅰ)![]() 天;(Ⅱ)
天;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)当![]() 时,
时, ,这时
,这时![]() 时,
时,![]() 显然符合题意,当
显然符合题意,当![]() 时,由
时,由![]() 可得
可得![]() ,由此可得到受益人天数;(Ⅱ)当投放的药剂质量为
,由此可得到受益人天数;(Ⅱ)当投放的药剂质量为![]() 时,
时, ,当
,当![]() 时,
时,![]()
![]() 在区间
在区间![]() 上单调递增,当
上单调递增,当![]() 时,由导数知识可知函数在
时,由导数知识可知函数在![]() 上单调递减,为使
上单调递减,为使![]() ,解不等式
,解不等式 可求
可求![]() 的取值范围,从而求出其最小值.
的取值范围,从而求出其最小值.
试题解析: (Ⅰ)当![]() 时,
时, ,…………………………2分
,…………………………2分
当![]() 时,
时,![]() 显然符合题意;………………………………3分
显然符合题意;………………………………3分
当![]() 时,由
时,由![]() 可得
可得![]() ;……………………………………5分
;……………………………………5分
综上![]() ,所以自来水达到有效净化一共可持续21天…………………………6分
,所以自来水达到有效净化一共可持续21天…………………………6分
(Ⅱ)由 ……………………………………7分
……………………………………7分
当![]() 时,
时,![]()
![]() 在区间
在区间![]() 上单调递增,所以
上单调递增,所以![]() ;………………2分
;………………2分
当![]() 时,
时,![]() ,所以函数在
,所以函数在![]() 上单调递减,从而得到
上单调递减,从而得到![]() ,
,
综上可知:![]() ,……………11分
,……………11分
为使![]() 恒成立,只要
恒成立,只要 即可,
即可,
所以![]() ,………………………12分
,………………………12分
所以应该投放的药剂质量![]() 的最小值为
的最小值为![]() .…………………………13分
.…………………………13分


科目:高中数学 来源: 题型:
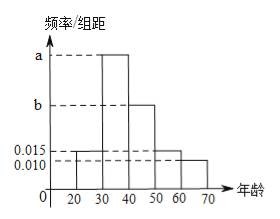
【题目】根据某电子商务平台的调查统计显示,参与调查的![]() 位上网购物者的年龄情况如右图.
位上网购物者的年龄情况如右图.
(1)已知![]() 、
、![]() 、
、![]() 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求![]() 的值;
的值;
(2)该电子商务平台将年龄在![]() 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放![]() 元的代金券,潜在消费人群每人发放
元的代金券,潜在消费人群每人发放![]() 元的代金券.已经采用分层抽样的方式从参与调查的
元的代金券.已经采用分层抽样的方式从参与调查的![]() 位上网购物者中抽取了
位上网购物者中抽取了![]() 人,现在要在这
人,现在要在这![]() 人中随机抽取
人中随机抽取![]() 人进行回访,求此三人获得代金券总和
人进行回访,求此三人获得代金券总和![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,函数
,函数![]() ,
,![]() (
(![]() 为自然对数的底数),且函数
为自然对数的底数),且函数![]() 的图象与函数
的图象与函数![]() 的图象在
的图象在![]() 处有公共的切线.
处有公共的切线.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)讨论函数![]() 的单调性;
的单调性;
(Ⅲ)证明:当![]() 时,
时,![]() 在区间
在区间![]() 内恒成立.
内恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.

(1)根据频率分布直方图,估计这50名学生百米测试成绩的平均值;
(2)若从第一组、第五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 和抛物线
和抛物线![]() 交于
交于![]() 两点,且直线
两点,且直线![]() 恰好通过椭圆
恰好通过椭圆![]() 的右焦点.
的右焦点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)经过椭圆![]() 右焦点的直线
右焦点的直线![]() 和椭圆
和椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 在椭圆上,且
在椭圆上,且![]() ,
,
其中![]() 为坐标原点,求直线
为坐标原点,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销量价格P(元)的关系如图所示;③每月需各种开支2 000元.
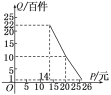
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com