练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某班50名学生在一次百米测试中，成绩全部介于13秒与18秒之间，将测试结果按如下方式分成五组：第一组，第二组，…，第五组，下图是按上述分组方法得到的频率分布直方图．

    （1）根据频率分布直方图，估计这50名学生百米测试成绩的平均值；

    （2）若从第一组、第五组中随机取出两个成绩，求这两个成绩的差的绝对值大于1的概率．

    【答案】（1）（2）

    【解析】

    试题分析：（1）频率分布直方图中利用组中值估计平均值：（2）先分别确定第一组、第五组中人数：成绩在的人数为人，成绩在的人数为人，再利用枚举法列出随机取出两个成绩的种数，共有21种情况，而其中这两个成绩的差的绝对值大于1包含12种情况，最后根据古典概率计算方法得概率

    试题解析：（1）由频率分布直方图知，百米测试成绩的平均值为

    ．．．．．．．．．．．．．．．．．．．．．．．．．5分

    （2）由频率分布直方图知，

    成绩在的人数为人，设为；．．．．．．．．．．．．．． 6分

    成绩在的人数为人，设为．．．．．．．．．．．7分

    若时，有3种情况；．．．．．．．．．．．．．．．．．．．．8分

    若时，有6种情况；．．．．．．．．．．．．．．．．．9分

    若分别在和内时，

    共有12种情况．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．． 11分

    所以基本事件总数为21种，事件“”所包含的基本事件个数有12种．

    ∴．．．．．．．．．．．．．．．．．．．．．．．．12分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】(本题满分15分)已知椭圆：过点，离心率为.

    （Ⅰ）求椭圆的标准方程；

    （Ⅱ）设分别为椭圆的左、右焦点，过的直线与椭圆交于不同两点，记的内切圆的面积为，求当取最大值时直线的方程，并求出最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在对人们休闲方式的一次调查中，共调查了124人，其中女性70人，男性54人，女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动．

    （Ⅰ）根据以上数据建立一个2×2列联表；

    （Ⅱ）能否在犯错误的概率不超过0.05的前提下认为性别与休闲方式有关系？

    附：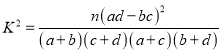

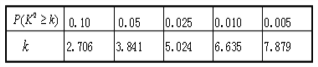
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点，点在轴上，点在轴的正半轴上，点在直线上，且满足

    （Ⅰ）当点在轴上移动时，求点的轨迹的方程；

    （Ⅱ）过点做直线与轨迹交于两点，若在轴上存在一点，使得是以点为直角顶点的直角三角形，求直线的斜率的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某中学联盟举行了一次“盟校质量调研考试”活动，为了解本次考试学生的某学科成绩情况，从中抽取部分学生的分数（满分为分，得分取正整数，抽取学生的分数均在之内）作为样本（样本容量为）进行统计，按照的分组作出频率分布直方图，并作出样本分数的茎叶图（茎叶图中仅列出了得分在的数据）

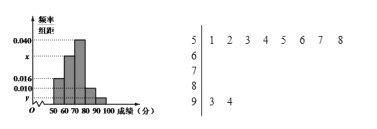
    （Ⅰ）求样本容量和频率分布直方图中的的值；

    （Ⅱ）在选取的样本中，从成绩在分以上（含分）的学生中随机抽取名学生参加“省级学科基础知识竞赛”，求所抽取的名学生中恰有一人得分在内的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地自来水苯超标，当地自来水公司对水质检测后，决定在水中投放一种药剂来净化水质，已知每投放质量为的药剂后，经过天该药剂在水中释放的浓度（毫克/升）满足，其中，当药剂在水中的浓度不低于5（毫克/升）时称为有效净化；当药剂在水中的浓度不低于5（毫克/升）且不高于10（毫克/升）时称为最佳净化.

    （Ⅰ）如果投放的药剂质量为，试问自来水达到有效净化一共可持续几天？

    （Ⅱ）如果投放的药剂质量为，为了使在9天（从投放药剂算起包括9天）之内的自来水达到最佳净化，试确定应该投放的药剂质量的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义：在数列中，若为常数）则称为“等方差数列”，下列是对“等方差数列”的有关判断（ ）

    ①若是“等方差数列”，在数列 是等差数列；

    ②是“等方差数列”；

    ③若是“等方差数列”，则数列为常）也是“等方差数列”；

    ④若既是“等方差数列”又是等差数列，则该数列是常数数列.

    其中正确命题的个数为( )

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，以为圆心，椭圆的短半轴长为半径的圆与直线相切.

    （1）求椭圆的标准方程；

    （2）已知点，和平面内一点，过点任作直线与椭圆相交于两点，设直线的斜率分别为，，试求满足的关系式.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】20名同学参加某次数学考试成绩（单位：分）的频率分布直方图如下：

    （Ⅰ）求频率分布直方图中的值；

    （Ⅱ）分别求出成绩落在， 中的学生人数；

    （Ⅲ）从成绩在的学生中任选2人，求此2人的成绩都在中的概率.

    查看答案和解析>>

    同步练习册答案