
【题目】设函数![]() ,
,![]() .
.
(1)求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)求证:方程![]() 有两个实数根;
有两个实数根;
(3)求证:![]() .
.
【答案】(1)![]() (2)证明见解析;(3)证明见解析;
(2)证明见解析;(3)证明见解析;
【解析】
(1)求导得到![]() ,再求得
,再求得![]() ,
,![]() ,写出切线方程.
,写出切线方程.
(2)令![]() ,求导
,求导![]() ,设
,设![]() ,则
,则![]() ,结合
,结合![]() ,得到
,得到![]() 在
在![]() 上单调递增,
上单调递增,![]() 在
在![]() 上单调递减,再利用零点存在定理求解.
上单调递减,再利用零点存在定理求解.
(3)设![]() ,则
,则![]() ,将证明
,将证明![]() ,转化为证明
,转化为证明![]() 成立,易知
成立,易知![]() 恒成立,则要证
恒成立,则要证![]() ,只需证
,只需证![]() 为单调递减函数,然后用导数法证明
为单调递减函数,然后用导数法证明![]() 即可.
即可.
(1)因为![]() ,
,
所以![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() 的图象在
的图象在![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
(2)设![]() ,定义域为
,定义域为![]() ,
,
![]() ,
,
设![]() ,
,
因为![]() ,所以
,所以![]() ,因此
,因此![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,所以
,所以![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
因此![]() ,而
,而![]() ,
,
所以![]() 在
在![]() 上有一个零点,
上有一个零点,
而![]() ,
,
所以![]() 在
在![]() 上有一个零点,
上有一个零点,
故方程![]() 有两个实数根.
有两个实数根.
(3)设![]() ,则
,则![]() ,
,
不等式![]() ,即为
,即为![]() ,
,
设![]()
![]()
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]()
所以![]()
所以![]() 恒成立,
恒成立,
所以要证![]() ,只需证
,只需证![]() 为单调递减函数.
为单调递减函数.
 ,
,
设![]()
![]()
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]()
所以![]() 恒成立,
恒成立,
则![]()
即![]() ,
,
所以![]() ,
,
所以![]() 为单调递减函数,
为单调递减函数,
故![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁、戊五人去参加数学、物理、化学三科竞赛,每个同学只能参加一科竞赛,若每个同学可以自由选择,则不同的选择种数是____;若甲和乙不参加同一科,甲和丙必须参加同一科,且这三科都有人参加,则不同的选择种数是_____.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点为
的焦点为![]() ,
,![]() ,P是椭圆C上一点.若椭圆C的离心率为
,P是椭圆C上一点.若椭圆C的离心率为![]() ,且
,且![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)求椭圆C的方程;
(2)已知O是坐标原点,向量![]() ,过点(2,0)的直线l与椭圆C交于M,N两点.若点
,过点(2,0)的直线l与椭圆C交于M,N两点.若点![]() 满足
满足![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周率π是数学中一个非常重要的数,历史上许多中外数学家利用各种办法对π进行了估算.现利用下列实验我们也可对圆周率进行估算.假设某校共有学生N人,让每人随机写出一对小于1的正实数a,b,再统计出a,b,1能构造锐角三角形的人数M,利用所学的有关知识,则可估计出π的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为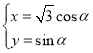 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,点
轴的正半轴为极轴,建立极坐标系,点![]() 的极坐标
的极坐标![]() ,直线
,直线![]() 经过点
经过点![]() ,且倾斜角为
,且倾斜角为![]() .
.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的标准参数方程;
的标准参数方程;
(2)直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,直线
两点,直线![]() 的参数方程为
的参数方程为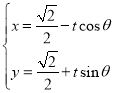 (t为参数),直线
(t为参数),直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求证:
两点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() 3,g(x)=alnx﹣2x(a∈R).
3,g(x)=alnx﹣2x(a∈R).
(1)讨论g(x)的单调性;
(2)是否存在实数a,使不等式f(x)≥g(x)恒成立?如果存在,求出a的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,且asinB=bsin(A+![]() ).
).
(1)求A;
(2)若b,![]() a,c成等差数列,△ABC的面积为2
a,c成等差数列,△ABC的面积为2![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国电子商务行业迎来了蓬勃发展的新机遇,但是电子商务行业由于缺乏监管,服务质量有待提高.某部门为了对本地的电商行业进行有效监管,调查了甲、乙两家电商的某种同类产品连续十天的销售额(单位:万元),得到如下茎叶图:
甲 | 乙 | |||||
7 | 5 | 10 | 7 | |||
9 | 5 | 3 | 11 | 5 | 7 | 8 |
8 | 6 | 12 | 3 | 5 | ||
4 | 2 | 13 | 2 | 6 | 9 | |
1 | 14 | 8 | ||||
(1)根据茎叶图判断甲、乙两家电商对这种产品的销售谁更稳定些?
(2)为了综合评估本地电商的销售情况,从甲、乙两家电商十天的销售数据中各抽取两天的销售数据,其中销售额不低于120万元的天数分别记为![]() ,令
,令![]() ,求随机变量Y的分布列和数学期望.
,求随机变量Y的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com