【题目】如图，一智能扫地机器人在A处发现位于它正西方向的B处和北偏东
方向上的C处分别有需要清扫的垃圾，红外线感应测量发现机器人到B的距离比到C的距离少0.4m，于是选择沿
路线清扫.已知智能扫地机器人的直线行走速度为0.2m/s,忽略机器人吸入垃圾及在B处旋转所用时间，10秒钟完成了清扫任务.
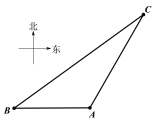
（1）B、C两处垃圾的距离是多少？（精确到0.1）
（2）智能扫地机器人此次清扫行走路线的夹角
是多少？（用反三角函数表示）
名师点拨卷系列答案
英才计划期末调研系列答案科目：高中数学 来源： 题型：
【题目】某省在2017年启动了“3+3”高考模式.所谓“3+3”高考模式，就是语文、数学、外语（简称语、数、外）为高考必考科目，从物理、化学、生物、政治、历史、地理（简称理、化、生、政、史、地）六门学科中任选三门作为选考科目.该省某中学2017级高一新生共有990人，学籍号的末四位数从0001到0990.
（1）现从高一学生中抽样调查110名学生的选考情况，问：采用什么样的抽样方法较为恰当?（只写出结论，不需要说明理由）
（2）据某教育机构统计，学生所选三门学科在将来报考专业时受限制的百分比是不同的.该机构统计了受限百分比较小的十二种选择的百分比值
，制作出如下条形图.
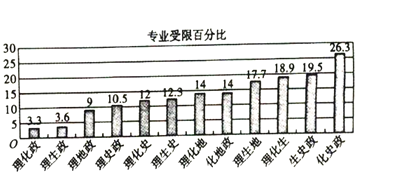
设以上条形图中受限百分比的均值为
，标准差为
.如果一个学生所选三门学科专业受限百分比在区间
内，我们称该选择为“恰当选择”.该校李明同学选择了化学，然后从余下五门选考科目中任选两门.问李明的选择为“恰当选择"的概率是多少?（均值，标准差均精确到0.1）
(参考公式和数据：
，
)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙两人同时参加一次数学测试，共有
道选择题，每题均有
个选项，答对得
分，答错或不答得
分．甲和乙都解答了所有的试题，经比较，他们只有
道题的选项不同，如果甲最终的得分为
分，那么乙的所有可能的得分值组成的集合为____________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数
（个）和温度
（
）的7组观测数据，其散点图如所示：
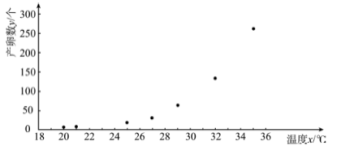
根据散点图，结合函数知识，可以发现产卵数和温度可用方程
来拟合，令
，结合样本数据可知
与温度可用线性回归方程来拟合．根据收集到的数据，计算得到如下值：
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中
，
．
（1）求和温度的回归方程（回归系数结果精确到
）；
（2）求产卵数关于温度的回归方程；若该地区一段时间内的气温在
之间（包括
与
），估计该品种一只昆虫的产卵数的范围.（参考数据：
，
，
，
，
．）
附：对于一组数据
，
，…，
，其回归直线
的斜率和截距的最小二乘估计分别为
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设
为数列
的前n项和, 且满足
为常数
.
（1）若
，求
的值；
（2）是否存在实数 
，使得数列为等差数列？若存在，求出的值；若不存在，请说明理由；
（3）当
时，若数列
满足
，且
，令
，求数列
的前n项和
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下图是一块平行四边形园地
，经测量，
.拟过线段
上一点
设计一条直路
（点
在四边形的边上，不计直路的宽度），将该园地分为面积之比为
的左，右两部分分别种植不同花卉.设
（单位：m）.
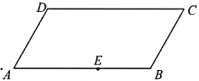
（1）当点与点
重合时，试确定点的位置；
（2）求
关于
的函数关系式；
（3）试确定点
的位置，使直路的长度最短.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，底面
为正方形，
底面，
，
为线段
的中点．
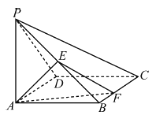
（1）若
为线段
上的动点，证明：平面
平面
；
（2）若为线段，
，
上的动点（不含
，
），
，三棱锥
的体积是否存在最大值？如果存在，求出最大值；如果不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
