如果已知bx2-4bx+2(a+c)=0(b≠0)有两个相等的实数根,求证a,b,c成等差数列.
【答案】
分析:本题考查的知识点是:韦达定理即一元二次方程根与系数的关系及等差数列的定义,要判断a,b,c成等差数列,即判断b-a=c-b,我们可以根据bx
2-4bx+2(a+c)=0(b≠0)有两个相等的实数根,结合韦达定理给出a,b,c之间的关系,进而得到答案.
解答:证明:∵已知bx
2-4bx+2(a+c)=0(b≠0)有两个相等的实数根,
∴(-4b)
2-4b•2(a+c)=0,
又∵b≠0,
∴2b-a-c=0,
即b-a=c-b.
故a,b,c成等差数列.
点评:代数的核心内容是函数,但由于函数、不等式、方程之间的辩证关系,故我们在解决函数问题是经常要用到方程的性质,其中韦达定理是最重要的方程的性质,其内容为:一元二次方程ax
2+bx+c=0(a≠0)的两个根分别为x
1,x
2,则
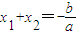
,
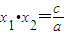

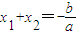 ,
,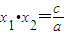


 名校课堂系列答案
名校课堂系列答案