
【题目】设函数![]()
![]() .若曲线
.若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的不等式
的不等式![]() 在(0,+
在(0,+![]() )上恒成立,求实数
)上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由函数![]() 的解析式得其定义域为
的解析式得其定义域为![]() .
.![]() . 因为曲线
. 因为曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,所以
,所以![]() ,
,![]() ,联立可得
,联立可得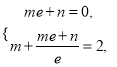 解方程组可得
解方程组可得![]() . 所以
. 所以![]() ,
, ![]() .分别解不等式
.分别解不等式![]() 与
与![]() ,可得单调递减与递增区间。(2)不等式
,可得单调递减与递增区间。(2)不等式![]() 恒成立即不等式
恒成立即不等式![]() 恒成立,构造函数
恒成立,构造函数![]() ,因为
,因为![]() ,所以对任意
,所以对任意![]() ,不等式
,不等式![]() 恒成立.考虑函数
恒成立.考虑函数![]() 的单调性。因为
的单调性。因为![]() 。当
。当![]() 时,对任意
时,对任意![]() 恒成立,此时函数
恒成立,此时函数![]() 单调递增.于是,不等式
单调递增.于是,不等式![]() 对任意
对任意![]() 恒成立,不符合题意;当函数
恒成立,不符合题意;当函数![]() 为减函数时,
为减函数时, ![]() ,即
,即![]() 恒成立时,函数
恒成立时,函数![]() 单调递减,构造函数
单调递减,构造函数![]() ,
, ![]() 大于函数
大于函数![]() 的最大值,求导数判断单调性,对任意
的最大值,求导数判断单调性,对任意![]() ,所以
,所以![]() ,即
,即![]() ,符合题意;当
,符合题意;当![]() 时,构造函数
时,构造函数![]() ,二次求导
,二次求导![]() ,令
,令![]() 得
得![]() ,因为
,因为![]() ,所以
,所以![]() 。所以当
。所以当![]() 时,
时, ![]() ,此时
,此时![]() 单调递增,所以
单调递增,所以![]()
![]() ,故当
,故当![]() 时,函数
时,函数![]() 单调递增.于是当
单调递增.于是当![]() 时,
时, ![]() 成立,不符合题意;综合上面三种情况可得所求。
成立,不符合题意;综合上面三种情况可得所求。
试题解析:解:(1)函数![]() 的定义域为
的定义域为![]() .
.
![]() .
.
依题意得![]() ,
, ![]() ,即
,即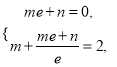
所以![]() .
.
所以![]() ,
, ![]() .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() .
.
(2)设函数![]() ,故对任意
,故对任意![]() ,不等式
,不等式![]() 恒成立.
恒成立.
又![]() ,当
,当![]() ,即
,即![]() 恒成立时,
恒成立时,
函数![]() 单调递减,设
单调递减,设![]() ,则
,则![]() ,
,
所以![]() ,即
,即![]() ,符合题意;
,符合题意;
当![]() 时,
时, ![]() 恒成立,此时函数
恒成立,此时函数![]() 单调递增.
单调递增.
于是,不等式![]() 对任意
对任意![]() 恒成立,不符合题意;
恒成立,不符合题意;
当![]() 时,设
时,设![]() ,
,
则![]()
![]() ;
;
当![]() 时,
时, ![]() ,此时
,此时![]() 单调递增,
单调递增,
所以![]()
![]() ,
,
故当![]() 时,函数
时,函数![]() 单调递增.
单调递增.
于是当![]() 时,
时, ![]() 成立,不符合题意;
成立,不符合题意;
综上所述,实数![]() 的取值范围为:
的取值范围为: ![]() .
.


科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他们各应偿还多少?已知牛、马、羊的主人各应偿还![]() 升,
升, ![]() 升,
升, ![]() 升,1斗为10升,则下列判断正确的是( )
升,1斗为10升,则下列判断正确的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣1)2+(y﹣2)2=25,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0(m∈R). 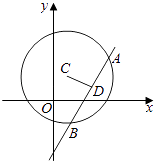
(1)求证:无论m取什么实数,直线l恒过第一象限;
(2)求直线l被圆C截得的弦长最短时m的值以及最短长度;
(3)设直线l与圆C相交于A、B两点,求AB中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB⊥AC,AB=BB1=1,B1C=2. 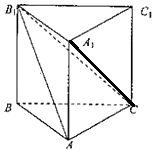
(1)求证:平面B1AC⊥平面ABB1A1;
(2)求直线A1C与平面B1AC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在![]() 轴上的圆
轴上的圆![]() 与直线
与直线![]() 切于点
切于点![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,经过原点,且斜率为正数的直线
,经过原点,且斜率为正数的直线![]() 与圆
与圆![]() 交于
交于![]() 两点.
两点.
(ⅰ)求证: ![]() 为定值;
为定值;
(ⅱ)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心为(1,1)的圆C经过点M(1,2).
(1)求圆C的方程;
(2)若直线x+y+m=0与圆C交于A、B两点,且△ABC是直角三角形,求实数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣4ax+b(a>0)在区间[0,1]上有最大值1和最小值﹣2.
(1)求a,b的值;
(2)若不等式f(x)≥mx在x∈(0,+∞)上恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2. (Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求平面PAD和平面PBE所成二面角(锐角)的余弦值.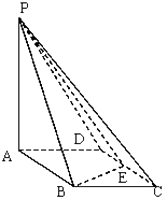
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com