
【题目】为调查大学生这个微信用户群体中每人拥有微信群的数量,现从武汉市大学生中随机抽取100位同学进行了抽样调查,结果如下:
微信群数量 | 频数 | 频率 |
0至5个 | 0 | 0 |
6至10个 | 30 | 0.3 |
11至15个 | 30 | 0.3 |
16至20个 | a | c |
20个以上 | 5 | b |
合计 | 100 | 1 |
(Ⅰ)求a,b,c的值;
(Ⅱ)以这100个人的样本数据估计武汉市的总体数据且以频率估计概率,若从全市大学生(数量很大)中随机抽取3人,记X表示抽到的是微信群个数超过15个的人数,求X的分布列和数学期望.
【答案】解:(Ⅰ)由已知得:0+30+30+a+5=100,解得a=35,
∴ ![]() .
.
(Ⅱ)依题意可知,微信群个数超过15个的概率为p= ![]() .
.
X的所有可能取值0,1,2,3.
则P(X=0)= ![]() ═
═ ![]() ,
,
P(X=1)= ![]() =
= ![]() ,
,
P(X=2)= ![]() =
= ![]() ,
,
P(X=3)= ![]() =
= ![]() .
.
其分布列如下:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
EX= ![]() =
= ![]()
【解析】(Ⅰ)由频率分布表能求出a,b,c的值.(Ⅱ)依题意可知,微信群个数超过15个的概率为p= ![]() . X的所有可能取值0,1,2,3.分别求出相应的概率,由此能求出X的分布列和EX.
. X的所有可能取值0,1,2,3.分别求出相应的概率,由此能求出X的分布列和EX.
【考点精析】根据题目的已知条件,利用离散型随机变量及其分布列的相关知识可以得到问题的答案,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,动物园要建造一面靠墙的两间相同的矩形熊猫居室,如果可供建造围墙的材料总长是![]() .
.
![]() 用宽
用宽![]() (单位
(单位![]() )表示所建造的每间熊猫居室的面积
)表示所建造的每间熊猫居室的面积![]() (单位
(单位![]() );
);
![]() 怎么设计才能使所建造的每间熊猫居室面积最大?并求出每间熊猫居室的最大面积?
怎么设计才能使所建造的每间熊猫居室面积最大?并求出每间熊猫居室的最大面积?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AA1=AB=2,AD=1点E,F,G分别是DD1 , AB,CC1的中点,则异面直线A1E与GF所成的角是( ) 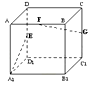
A.90°
B.60°
C.45°
D.30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() .
.
(1)若直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,当
,当![]() 时,求
时,求![]() 的值;
的值;
(2)若![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作圆
作圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点?若过定点则求出该定点,若不存在则说明理由;
是否过定点?若过定点则求出该定点,若不存在则说明理由;
(3)若![]() 为圆
为圆![]() 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为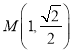 ,求四边形
,求四边形![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,甲、乙是边长为![]() 的两块正方形钢板,现要将甲裁剪焊接成一个正四棱柱,将乙裁剪焊接成一个正四棱锥,使它们的全面积都等于一个正方形的面积(不计焊接缝的面积).
的两块正方形钢板,现要将甲裁剪焊接成一个正四棱柱,将乙裁剪焊接成一个正四棱锥,使它们的全面积都等于一个正方形的面积(不计焊接缝的面积).
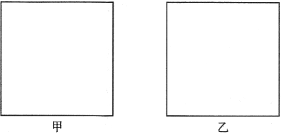
(1)将你的裁剪方法用虚线标示在图中,并作简要说明;
(2)试比较你所制作的正四棱柱与正四棱锥体积的大小,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com