
【题目】如图所示,正四棱椎P-ABCD中,底面ABCD的边长为2,侧棱长为![]() .
.

(I)若点E为PD上的点,且PB∥平面EAC.试确定E点的位置;
(Ⅱ)在(I)的条件下,点F为线段PA上的一点且![]() ,若平面AEC和平面BDF所成的锐二面角的余弦值为
,若平面AEC和平面BDF所成的锐二面角的余弦值为![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(I)E为PD中点,(Ⅱ)![]()
【解析】
(Ⅰ)设BD交AC于点O,连结OE推导出PB∥OE,由O为BD的中点,推导出在△BDP中,E为PD中点.
(Ⅱ)连结OP,以O为原点,OC、OD、OP所成直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出λ.
(Ⅰ)设BD交AC于点O,连结OE,
∵PB∥平面AEC,平面AEC∩平面BDP=OE,
∴PB∥OE,
又O为BD的中点,
∴在△BDP中,E为PD中点.
(Ⅱ)连结OP,由题意得PO⊥平面ABCD,且AC⊥BD,
∴以O为原点,OC、OD、OP所成直线为x,y,z轴,建立空间直角坐标系,
OP![]() ,
,
∴A(![]() ,0,0),B(0,
,0,0),B(0,![]() ,0),C(
,0),C(![]() ,0,0),D(0,
,0,0),D(0,![]() ,0),P(0,0,
,0),P(0,0,![]() ),
),
则E(0,![]() ,
,![]() ),
),![]() (
(![]() ,0,0),
,0,0),![]() (
(![]() ,
,![]() ,
,![]() ),
),![]() (0,
(0,![]() ,0),
,0),
设平面AEC的法向量![]() (x,y,z),
(x,y,z),
则 ,令z=1,得平面AEC的一个法向量
,令z=1,得平面AEC的一个法向量![]() (0,
(0,![]() ,1),
,1),
设平面BDF的法向量![]() (x,y,z),
(x,y,z),
由![]() ,得F(
,得F(![]() ,0,
,0,![]() ),
),![]() (
(![]() ,
,![]() ,
,![]() ),
),
∴ ,令z=1,得
,令z=1,得![]() (
(![]() ,0,1),
,0,1),
∵平面AEC和平面BDF所成的锐二面角的余弦值为![]() ,
,
∴cos ,
,
解得λ![]() .
.


科目:高中数学 来源: 题型:
【题目】已知高中学生的数学成绩与物理成绩具有线性相关关系,在一次考试中某班7名学生的数学成绩与物理成绩如下表:
数学成绩 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理成绩 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
(1)求这7名学生的数学成绩的极差和物理成绩的平均数;
(2)求物理成绩![]() 对数学成绩
对数学成绩![]() 的线性回归方程;若某位学生的数学成绩为110分,试预测他的物理成绩是多少?
的线性回归方程;若某位学生的数学成绩为110分,试预测他的物理成绩是多少?
下列公式与数据可供参考:
用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: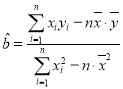 ,
,![]() ;
;
![]() ,
,![]() ,
,
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着共享单车的成功运营,更多的共享产品逐步走人大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷,某公司随机抽取1000人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的1000人中的性别以及意见进行了分类,得到的数据如下表所示:
男 | 女 | 总计 | |
认为共享产品对生活有益 |
|
|
|
认为共享产品对生活无益 |
|
|
|
总计 |
|
|
|
(1)求出表格中![]() 的值,并根据表中的数据,判断能否在犯错误的概率不超过
的值,并根据表中的数据,判断能否在犯错误的概率不超过![]() 的前提下,认为对共享产品的态度与性别有关系?
的前提下,认为对共享产品的态度与性别有关系?
(2)现按照分层抽样从认为共享产品对生活无益的人员中随机抽取6人,再从6人中随机抽取2人赠送超市购物券作为答谢,求恰有1人是女性的概率.
参考公式: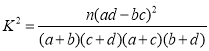 .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程:
已知极坐标系的极点在直角坐标系的原点,极轴与x轴非负半轴重合,直线l的参数方程为:![]() (t为参数,a∈[0,π),曲线C的极坐标方程为:p=2cosθ.
(t为参数,a∈[0,π),曲线C的极坐标方程为:p=2cosθ.
(Ⅰ)写出曲线C在直角坐标系下的标准方程;
(Ⅱ)设直线l与曲线C相交PQ两点,若|PQ|![]() ,求直线l的斜率.
,求直线l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司准备在2020年年初将两千万投资东营经济开发区的“示范区”新型物流,商旅文化两个项目中的一个之中.
项目一:新型物流仓是为企业提供仓储、运输、配送、货运信息等综合物流服务的平台.现准备投资建设10个新型物流仓,每个物流仓投资0.2千万元,假设每个物流仓盈利是相互独立的,据市场调研,到2022年底每个物流仓盈利的概率为![]() ,若盈利则盈利为投资额的40%,否则盈利额为0.
,若盈利则盈利为投资额的40%,否则盈利额为0.
项目二:购物娱乐广场是一处融商业和娱乐于一体的现代化综合服务广场.据市场调研,投资到该项目上,到2022年底可能盈利投资额的50%,也可能亏损投资额的30%,且这两种情况发生的概率分别为![]() 和
和![]() .
.
(1)若投资项目一,记![]() 为盈利的物流仓的个数,求
为盈利的物流仓的个数,求![]() (用
(用![]() 表示);
表示);
(2)若投资项目二,记投资项目二的盈利为![]() 千万元,求
千万元,求![]() (用
(用![]() 表示);
表示);
(3)在(1)(2)两个条件下,针对以上两个投资项目,请你为投资公司选择一个项目,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C:![]() 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足![]() .
.
(1)求点P的轨迹方程;
(2)设点Q在直线![]() 上,且
上,且![]() 。证明:过点P且垂直于OQ的直线l过C的左焦点F.
。证明:过点P且垂直于OQ的直线l过C的左焦点F.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com