
【题目】已知函数![]() .
.
(I)已知函数![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(Ⅱ)若函数![]() 在
在![]() 上无零点,求
上无零点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(I)求出![]() ,然后由条件建立方程求解即可;
,然后由条件建立方程求解即可;
(Ⅱ)求出![]() ,然后分
,然后分![]() 、
、![]() 、
、![]() 、
、![]() 四种情况讨论,每种情况下求出
四种情况讨论,每种情况下求出![]() 在
在![]() 上的单调性,然后结合其最值求解即可.
上的单调性,然后结合其最值求解即可.
(I)由题意可得![]() ,∴
,∴![]() ,
,
又因为函数![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,
垂直,
所以![]() ,∴
,∴![]() .
.
(Ⅱ)由题意可知![]() ,
,
当![]() 时,
时,![]() ,所以,
,所以,![]() 在
在![]() 上单调递减,
上单调递减,
即![]() 在
在![]() 上单调递减.又因为
上单调递减.又因为![]() ,
,
所以![]() 在
在![]() 上无零点.即
上无零点.即![]() 满足条件.
满足条件.
当![]() 时,令
时,令![]() 得
得![]() ,
,![]() (舍),
(舍),
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,有
上单调递减,有![]() ,
,
此时![]() 在
在![]() 上无零点,即
上无零点,即![]() 时满足条件.
时满足条件.
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
当且仅当![]() 且
且![]() 时,
时,![]() 在
在![]() 上无零点,
上无零点,
解得![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
当且仅当![]() 且
且![]() 时,
时,![]() 在
在![]() 上无零点,此时无解.
上无零点,此时无解.
综上所得:![]()


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
【题目】如图所示,正四棱椎P-ABCD中,底面ABCD的边长为2,侧棱长为![]() .
.

(I)若点E为PD上的点,且PB∥平面EAC.试确定E点的位置;
(Ⅱ)在(I)的条件下,点F为线段PA上的一点且![]() ,若平面AEC和平面BDF所成的锐二面角的余弦值为
,若平面AEC和平面BDF所成的锐二面角的余弦值为![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了![]() 位育龄妇女,结果如表.
位育龄妇女,结果如表.
非一线 | 一线 | 总计 | |
愿生 |
|
|
|
不愿生 |
|
|
|
总计 |
|
|
|
附表:
|
|
|
|
|
|
|
|
由![]() 算得,
算得,![]() 参照附表,得到的正确结论是( )
参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过![]() 的前提下,认为“生育意愿与城市级别有关”
的前提下,认为“生育意愿与城市级别有关”
B. 有![]() 以上的把握认为“生育意愿与城市级别有关”
以上的把握认为“生育意愿与城市级别有关”
C. 在犯错误的概率不超过![]() 的前提下,认为“生育意愿与城市级别无关”
的前提下,认为“生育意愿与城市级别无关”
D. 有![]() 以上的把握认为“生育意愿与城市级别无关”
以上的把握认为“生育意愿与城市级别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年“双十一”期间,某商场举办了一次有奖促销活动,顾客消费每满1000元可参加一次抽奖(例如:顾客甲消费930元,不得参与抽奖;顾客乙消费3400元,可以抽奖三次)。如图1,在圆盘上绘制了标有A,B,C,D的八个扇形区域,每次抽奖时由顾客按动按钮使指针旋转一次,旋转结束时指针会随机停在圆盘上的某一个位置,顾客获奖的奖次由指针所指区域决定(指针与区域边界线粗细忽略不计)。商家规定:指针停在标A,B,C,D的扇形区域分别对应的奖金为200元、150元、100元和50元。已知标有A,B,C,D的扇形区域的圆心角成等差数列,且标D的扇形区域的圆心角是标A的扇形区域的圆心角的4倍.
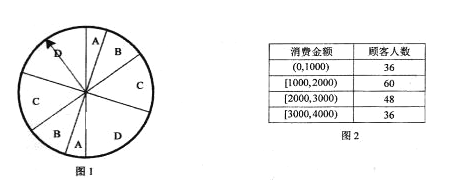
(I)某顾客只抽奖一次,设该顾客抽奖所获得的奖金数为X元,求X的分布列和数学期望;
(II)如图2,该商场统计了活动期间一天的顾客消费情况.现按照消费金额分层抽样选出15位顾客代表,其中获得奖金总数不足100元的顾客代表有7位.现从这7位顾客代表中随机选取两位,求这两位顾客的奖金总数和仍不足100元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2011年,国际数学协会正式宣布,将每年的3月14日设为“国际数学节”,其来源是中国古代数学家祖冲之的圆周率,为庆祝该节日,某校举办的“数学嘉年华”活动中,设计了如下的有奖闯关游戏:参赛选手按第一关、第二关、第三关的顺序依次闯关,若闯关成功,则分别获得5个、10个、20个学豆的奖励.游戏还规定:当选手闯过一关后,可以选择带走相应的学豆,结束游戏;也可以选择继续闯下一关,若有任何一关没有闯关成功,则全部学豆归零,游戏结束.设选手甲能闯过第一关、第二关、第三关的概率分别为![]() ,选手选择继续闯关的概率均为
,选手选择继续闯关的概率均为![]() ,且各关之间闯关成功与否互不影响.
,且各关之间闯关成功与否互不影响.
(1)求选手甲第一关闯关成功且所得学豆为零的概率;
(2)设该选手所得学豆总数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | 不大于2000元 | 大于2000元 |
仅使用A | 27人 | 3人 |
仅使用B | 24人 | 1人 |
(Ⅰ)估计该校学生中上个月A,B两种支付方式都使用的人数;
(Ⅱ)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于2000元的概率;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现他本月的支付金额大于2000元.结合(Ⅱ)的结果,能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆锥![]() (其中
(其中![]() 为顶点,
为顶点,![]() 为底面圆心)的侧面积与底面积的比是
为底面圆心)的侧面积与底面积的比是![]() ,则圆锥
,则圆锥![]() 与它外接球(即顶点在球面上且底面圆周也在球面上)的体积比为( )
与它外接球(即顶点在球面上且底面圆周也在球面上)的体积比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像相邻两条对称轴间的距离为
的图像相邻两条对称轴间的距离为![]() ,且
,且![]() ,则以下命题中为假命题的是( )
,则以下命题中为假命题的是( )
A.函数![]() 在
在![]() 上是增函数.
上是增函数.
B.函数![]() 图像关于点
图像关于点![]() 对称
对称
C.函数![]() 的图象可由
的图象可由![]() 的图象向左平移
的图象向左平移![]() 个单位长度得到
个单位长度得到
D.函数![]() 的图象关于直线
的图象关于直线![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
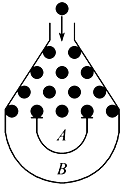
【题目】某超市春节大酬宾,购物满100元可参加一次抽奖活动,规则如下:顾客将一个半径适当的小球放入如图所示的容器正上方的人口处,小球在自由落下的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,顾客相应获得袋子里的奖品.已知小球每次遇到黑色障碍物时,向左向右下落的概率都为![]() .若活动当天小明在该超市购物消费108元,按照活动规则,他可参加一次抽奖,则小明获得A袋中的奖品的概率为_____.
.若活动当天小明在该超市购物消费108元,按照活动规则,他可参加一次抽奖,则小明获得A袋中的奖品的概率为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com