
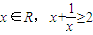 恒成立;
恒成立; 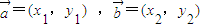 ,则
,则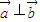 ?x1•x2+y1•y2=0;
?x1•x2+y1•y2=0;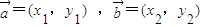 ,则
,则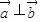 ?x1•x2+y1•y2=0,正确;对于④由Sn+1>Sn,则an+1>0,不一定是an+1>an,故不正确.⑤a=3时,可检验两直线平行且不重合,但当两直线平行且不重合时,经检验,a=0和a=1不成立,由一次项系数之比相等但不等于常数项之比,求得a=3,故可得答案.
?x1•x2+y1•y2=0,正确;对于④由Sn+1>Sn,则an+1>0,不一定是an+1>an,故不正确.⑤a=3时,可检验两直线平行且不重合,但当两直线平行且不重合时,经检验,a=0和a=1不成立,由一次项系数之比相等但不等于常数项之比,求得a=3,故可得答案.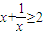 不成立,故不正确;对于②,因为△ABC中,当sinA=sinB时,A=B或A+B=π,故三角形是等腰三角形,故正确.对于③若向量
不成立,故不正确;对于②,因为△ABC中,当sinA=sinB时,A=B或A+B=π,故三角形是等腰三角形,故正确.对于③若向量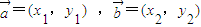 ,则
,则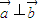 ?x1•x2+y1•y2=0,正确;
?x1•x2+y1•y2=0,正确;

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
A、若x∈R且x≠0,则x+
| ||
| B、在△ABC中,若sin2A=sin2B,则△ABC是等腰三角形 | ||
| C、对等差数列{an}的前n项和Sn,若对任意正整数n都有Sn+1>Sn,则an+1>an对任意正整数n恒成立 | ||
| D、a=3是直线ax+2y+3a=0与直线3x+(a-1)y=a-7平行且不重合的充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com