
(I)证明![]() 为常数;
为常数;
(Ⅱ)若动点![]() (其中
(其中![]() 为坐标原点),求点
为坐标原点),求点![]() 的轨迹方程.
的轨迹方程.
解:由条件知F(2,0),设A(x1,y1),B(x2,y2).
(I)当AB与x轴垂直时,可设点A、B的坐标分别为(2, ![]() )、(2,-
)、(2,-![]() ),
),
此时![]() ·
·![]() =(1,
=(1,![]() )·(1,-
)·(1,-![]() )=-1.
)=-1.
当AB不与x轴垂直时,设直线AB的方程是y=k(x-2)(k≠±1).
代入x2-y2=2有(1-k2)x2+4k2x-(4k2+2)=0.
则x1,x2是上述方程的两个实根,所以![]()
于是![]() ·
·![]() =(x1-1)(x2-1)+y1y2=(x1-1)(x2-1)+k2(x1-2)(x2-2)=(k2+1)x1x2-(2k2+1)(x1+x2)+4k2+1 =
=(x1-1)(x2-1)+y1y2=(x1-1)(x2-1)+k2(x1-2)(x2-2)=(k2+1)x1x2-(2k2+1)(x1+x2)+4k2+1 =![]() +4k2+1=(-4k2-2)+4k2+1=-1.
+4k2+1=(-4k2-2)+4k2+1=-1.
综上所述,![]() ·
·![]() 为常数-1.
为常数-1.
(Ⅱ)解法一 设M(x,y),则![]() =(x-1,y),
=(x-1,y),![]() =(x1-1,y1),
=(x1-1,y1),![]() =(x2-1,y2),
=(x2-1,y2),![]() =(-1,0).由
=(-1,0).由![]() =
=![]() +
+![]() +
+![]() 得:
得: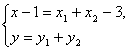 即
即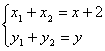
于是AB的中点坐标为(![]() ).
).
当AB不与x轴垂直时,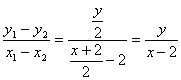 ,即y1-y2=
,即y1-y2=![]() (x1-x2),
(x1-x2),
又因为A、B两点在双曲线上,所以![]() 两式相减得
两式相减得
(x1-x2)(x1+x2)=(y1-y2)(y1+y2),即(x1-x2)(x+2)=(y1-y2)y.
将y1-y2=![]() (x1-x2)代入上式,化简得x2-y2=4.
(x1-x2)代入上式,化简得x2-y2=4.
当AB与x轴垂直时,x1=x2=2,求得M(2,0),也满足上述方程.
所以点M的轨迹方程是x2-y2=4.
解法二 同解法一得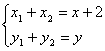 ①
①
当AB不与x轴垂直时,由(Ⅰ)有x1+x2=![]() , ②
, ②
y1+y2=k(x1+x2-4)=k(![]() -4)=
-4)= ![]() . ③
. ③
由①、②、③得x+2=![]() ,④ y=
,④ y=![]() ⑤
⑤
当k≠0时,y≠0,由④、⑤得,![]() =k,将其代入⑤有y=
=k,将其代入⑤有y=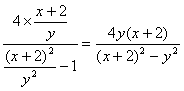 ,整理得x2-y2=4.
,整理得x2-y2=4.
当k=0时,点M的坐标为(-2,0),满足上述方程.
当AB与x轴垂直时,x1=x2=2,求得M(2,0),也满足上述方程.
故点M的轨迹方程是x2-y2=4.


科目:高中数学 来源: 题型:
| 4 |
| 3 |
| x2 |
| 5 |
| y2 |
| 20 |
| 1 |
| 4a |
| x2 |
| 4 |
| y2 |
| m |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 5 |
| y2 |
| 20 |
| 1 |
| 4a |
| x2 |
| 4-k |
| y2 |
| k-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com